题目内容
9.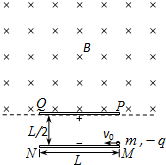 如图所示,MN、PQ是平行带电长金属板,板长为L,两板间距离为$\frac{L}{2}$,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从负极板MN边缘M点沿平行于板的方向从右向左射入两板间,结果粒子恰好从正极板PQ左边缘Q点飞进磁场,然后又恰好从PQ板的右边缘P点飞进电场,直到飞出电场.不计粒子的重力,试求:
如图所示,MN、PQ是平行带电长金属板,板长为L,两板间距离为$\frac{L}{2}$,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从负极板MN边缘M点沿平行于板的方向从右向左射入两板间,结果粒子恰好从正极板PQ左边缘Q点飞进磁场,然后又恰好从PQ板的右边缘P点飞进电场,直到飞出电场.不计粒子的重力,试求:(1)两金属板间匀强电场的电场强度大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子从飞进电场到最后离开电场运动的总时间.
分析 (1)带电粒子在平行金属板间做的是类平抛运动,对物体受力分析,根据平抛运动的规律可以求得电场的场强大小;
(2)带电粒子以速度v飞出电场后射入匀强磁场做匀速圆周运动,根据粒子的运动画出运动的轨迹,由几何关系可以求得磁感强度的大小;
(3)根据粒子做类平抛运动的时间和粒子在磁场中做匀速圆周运动的时间求出总时间.
解答 解:(1)粒子飞进电场做类平抛运动,从M点到Q点的时间为t1,
由位移公式可知:L=v0t1,$\frac{L}{2}=\frac{1}{2}at_1^2$,
由牛顿第二定律得:qE=ma,
由上面三式解得:$E=\frac{mv_0^2}{qL}$;
(2)设粒子飞进磁场时,速度大小为v,速度方向与水平成θ角,
则:$tanθ=\frac{{a{t_1}}}{v_0}=1$,解得:θ=450,
速度大小:$v=\sqrt{2}{v_0}$,
粒子在磁场中做圆周运动,其圆心角为$\frac{3π}{2}$,
由几何知识可得,轨道半径:r=$\frac{{\sqrt{2}}}{2}L$,
由牛顿第二定律得:$qvB=\frac{{m{v^2}}}{r}$,
解得:$B=\frac{{2m{v_0}}}{qL}$;
(3)粒子在磁场中做圆周运动时间:${t_2}=\frac{3T}{4}=\frac{3πL}{{4{v_0}}}$,
粒子从飞进电场到最后离开电场运动的总时间:$t={t_1}+{t_2}+{t_1}=(2+\frac{3π}{4})\frac{L}{v_0}$;
答:(1)两金属板间匀强电场的电场强度大小为$\frac{m{v}_{0}^{2}}{qL}$;
(2)匀强磁场的磁感应强度B的大小为$\frac{2m{v}_{0}}{qL}$;
(3)粒子从飞进电场到最后离开电场运动的总时间为(2+$\frac{3π}{4}$)$\frac{L}{{v}_{0}}$.
点评 本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案| A. | 火车通过站牌的速度是50km/h | |
| B. | 汽车从泉州行驶到深沪的速度是18m/s | |
| C. | 子弹从枪口飞出的速度是800m/s | |
| D. | 汽车速度计显示的速度为70km/h |
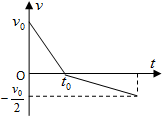 从地面以速率v0竖直上抛一个质量为m的小球,由于受到大小恒定的空气阻力作用,小球落回地面的速率减为$\frac{{v}_{0}}{2}$,以竖直向上为正方向,该运动过程的速度--时间图象如图所示.关于该过程,下列说法正确的是( )
从地面以速率v0竖直上抛一个质量为m的小球,由于受到大小恒定的空气阻力作用,小球落回地面的速率减为$\frac{{v}_{0}}{2}$,以竖直向上为正方向,该运动过程的速度--时间图象如图所示.关于该过程,下列说法正确的是( )| A. | 空气阻力大小为小球重力的$\frac{3}{4}$倍 | |
| B. | 上升过程与下降过程中加速度大小之比为4:1 | |
| C. | 上升过程与下降过程中合力对小球做功之比为2:1 | |
| D. | 上升过程与下降过程中克服空气阻力做功的功率之比为1:1 |
| A. | 气体自发的扩散运动总是沿着分子热运动的无序性增大的方向进行 | |
| B. | 满足能量守恒定律的过程都可以自发地进行 | |
| C. | 一定质量的理想气体,当温度不变时,压强增大,分子的密集程度也增大 | |
| D. | 通过有限的过程可以把一个物体冷却到绝对零度 |
 如图所示,通与电流I的直导线MN固定在竖直位置上,且与导线框abcd在同一平面内,则在下列情况下,导线框中不能产生感应电流的是( )
如图所示,通与电流I的直导线MN固定在竖直位置上,且与导线框abcd在同一平面内,则在下列情况下,导线框中不能产生感应电流的是( )| A. | 通过直导线的电流强度增大 | B. | 通过直导线的电流强度减小 | ||
| C. | 线框水平向右移动 | D. | 线框水平向下移动 |
| A. | 透过平行于日光灯的窄缝看正常发光的日光灯时能观察到彩色条纹,这是光的色散现象 | |
| B. | 在光的双缝干涉实验中,若仅将入射光由绿光改为黄光,则条纹间距变宽 | |
| C. | 用光导纤维束传送图象信息,这是光的衍射的应用 | |
| D. | 光的偏振现象说明光是一种纵波 |
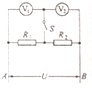 如图所示的电路中,R1=R2=2kΩ,电压表V1的内阻为6kΩ,电压表V2的内阻为3kΩ,AB间的电压U保持不变.当电键S闭合后.它们的示数变化是( )
如图所示的电路中,R1=R2=2kΩ,电压表V1的内阻为6kΩ,电压表V2的内阻为3kΩ,AB间的电压U保持不变.当电键S闭合后.它们的示数变化是( )| A. | V1表的示数变小,V2表的示数变大 | B. | V1表的示数变大,V2表的示数变小 | ||
| C. | V1,V2表的示数均变小 | D. | V1,V2表的示数均变大 |
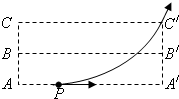 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求:
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求: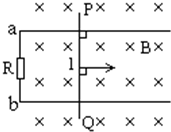 如图,光滑金属导轨宽度为L=0.2m,一根长直导线在磁感应强度B=1T的匀强磁场中以V=5m/s的速度做切割磁感线运动,直导线垂直于磁感线,运动方向跟磁感线、直导线垂直.求:
如图,光滑金属导轨宽度为L=0.2m,一根长直导线在磁感应强度B=1T的匀强磁场中以V=5m/s的速度做切割磁感线运动,直导线垂直于磁感线,运动方向跟磁感线、直导线垂直.求: