题目内容
12.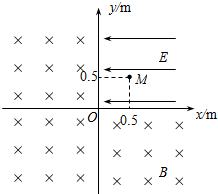 如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,方向水平向左的匀强电场,其余三象限分布着垂直纸面向里的匀强磁场.现从电场中M(0.5,0.5)点由静止释放一重力不计的带正电粒子,粒子的电荷量q=2×10-4C,质量m=1×10-8kg,该粒子第一次进入磁场后将垂直通过x轴.求:
如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,方向水平向左的匀强电场,其余三象限分布着垂直纸面向里的匀强磁场.现从电场中M(0.5,0.5)点由静止释放一重力不计的带正电粒子,粒子的电荷量q=2×10-4C,质量m=1×10-8kg,该粒子第一次进入磁场后将垂直通过x轴.求:(1)匀强磁场的磁感应强度大小;
(2)带电粒子第二次进入磁场时的位置坐标;
(3)在粒子第二次进入磁场时,撤掉第I象限的电场,粒子在磁场中运动后又进入第I象限且经过释放点M,则粒子从M点由静止释放到再经过M点所用的总时间是多少.
分析 带电粒子在匀强电场中做的是类平抛运动,利用平抛运动规律,结合电场强度、电荷的荷质比,求出粒子的进入磁场的速度大小与方向以及位置.当带电粒子进入磁场后,仅受洛伦兹力作用,做匀速圆周运动.由微粒第一次进入磁场后将垂直通过x轴,可寻找到已知长度与圆弧半径的关系,从而求出磁感应强度,当粒子再次进入电场时,仍是类平抛运动.利用相同方法求出离开电场的位置.
要求微粒从释放到回到M点所用时间,画出带电粒子的运动轨迹,当粒子做类平抛运动,运用平抛运动规律求出时间,当粒子做匀速圆周运动时,由周期公式求出运动时间.
解答 解:(1)根据动能定理得:qExM=$\frac{1}{2}$mv2-0,
解得:v=$\sqrt{\frac{2qE{x}_{M}}{m}}$=1×104m/s,
因为微粒第一次进入磁场后将垂直通过x轴,根据几何关系知,粒子在磁场中做圆周运动的半径R=xm,
R=xM=$\frac{mv}{qB}$,
解得:B=$\frac{mv}{q{x}_{M}}$=$\frac{1×1{0}^{4}}{2×1{0}^{4}×0.5}$=1T;
(2)粒子垂直进入电场,做类平抛运动,
由牛顿第二定律得:a抛=$\frac{qE}{m}$=1×108m/s2,
xM=$\frac{1}{2}$a抛t抛2,
解得:t抛=10-4s,
则:y=vt抛=104×10-4=1m,
带电微粒第二次进入磁场时的位置坐标为(0m,1m);
(3)第一次进入磁场后轨迹如图所示,入磁场时:
vM=a抛t抛=108×10-4=104m/s,
v入=$\sqrt{{v}^{2}+{v}_{x}^{2}}$=$\sqrt{2}$×104m/s,
粒子轨道半径:R′=$\frac{m{v}_{入}}{qB}$=$\frac{1}{\sqrt{2}}$m,轨迹如图所示,
粒子运动时间:t=2×$\frac{3}{4}$T+2t抛+$\frac{{L}_{OM}}{{v}_{入}}$=$\frac{3πm}{qB}$+2t抛+$\frac{0.5\sqrt{2}}{{v}_{入}}$,
解得:t=7.21×10-4s.
答:(1)匀强磁场的磁感应强度为1T;
(2)带电微粒第二次进入磁场时的位置坐标为(0m,1m);
(3)为了使微粒还能回到释放点M,在微粒第二次进入磁场后撤掉第Ⅰ象限的电场,求此情况下微粒从释放到回到M点所用时间为7.21×10-4s.
点评 本题重点是画出带电粒子的运动轨迹,当是平抛运动时,则可分解成沿电场强度方向是匀加速,垂直电场强度方向是匀速.当是圆周运动时,可由几何关系去找到已知长度与半径的关系,最终能求出结果.

| A. | 零时刻过中性面,感应电动势的瞬时值表达式e=311Sin100πt V | |
| B. | 每秒内,线圈经过中性面50次 | |
| C. | 若线圈匝数为100,穿过线圈的最大磁通量为0.01Wb | |
| D. | 线圈从中性面转过90度的过程中,电动势的平均值是220V |
 2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,下列说法正确的是( )
2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,下列说法正确的是( )| A. | 神舟八号的加速度比天宫一号的加速度大 | |
| B. | 神舟八号的运行速度比天宫一号的运行速度大 | |
| C. | 神舟八号的运行周期比天宫一号的运行周期长 | |
| D. | 神舟八号通过加速后变轨可实现与天宫一号对接 |
 从地面以速率v0竖直上抛一个质量为m的小球,由于受到大小恒定的空气阻力作用,小球落回地面的速率减为$\frac{{v}_{0}}{2}$,以竖直向上为正方向,该运动过程的速度--时间图象如图所示.关于该过程,下列说法正确的是( )
从地面以速率v0竖直上抛一个质量为m的小球,由于受到大小恒定的空气阻力作用,小球落回地面的速率减为$\frac{{v}_{0}}{2}$,以竖直向上为正方向,该运动过程的速度--时间图象如图所示.关于该过程,下列说法正确的是( )| A. | 空气阻力大小为小球重力的$\frac{3}{4}$倍 | |
| B. | 上升过程与下降过程中加速度大小之比为4:1 | |
| C. | 上升过程与下降过程中合力对小球做功之比为2:1 | |
| D. | 上升过程与下降过程中克服空气阻力做功的功率之比为1:1 |
| A. | 气体自发的扩散运动总是沿着分子热运动的无序性增大的方向进行 | |
| B. | 满足能量守恒定律的过程都可以自发地进行 | |
| C. | 一定质量的理想气体,当温度不变时,压强增大,分子的密集程度也增大 | |
| D. | 通过有限的过程可以把一个物体冷却到绝对零度 |
 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求:
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求: 如图,光滑金属导轨宽度为L=0.2m,一根长直导线在磁感应强度B=1T的匀强磁场中以V=5m/s的速度做切割磁感线运动,直导线垂直于磁感线,运动方向跟磁感线、直导线垂直.求:
如图,光滑金属导轨宽度为L=0.2m,一根长直导线在磁感应强度B=1T的匀强磁场中以V=5m/s的速度做切割磁感线运动,直导线垂直于磁感线,运动方向跟磁感线、直导线垂直.求: