题目内容
有一摆钟的摆长为L1时，在某一标准时间内快a分钟，若摆长为L2时，在同一标准时间内慢b分钟，求为使其准确，摆长应为多长？（可把钟摆视为摆角很小的单摆）
l=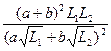
.
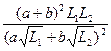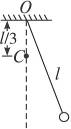
.解法一：设该标准时间为t s，准确摆钟摆长为L m，走时快的钟周期为T1 s，走时慢的钟周期为T2 s，准确的钟周期为T s.不管走时准确与否，钟摆每完成一次全振动，钟面上显示的时间都是T s.
由各摆钟在t s内钟面上显示的时间求解
对快钟：t+60a=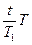
①
对慢钟：t-60b=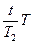
②
联立解①②式，可得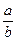
=
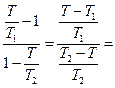
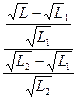
最后可得L=.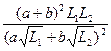
解法二：由各摆钟在t s内的振动次数关系求
设快钟在t s内全振动次数为n1，慢钟为n2，准确的钟为n0.显然，快钟比准确的钟多振动了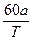
次，慢钟比准确的钟少振动了
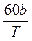次，故：
对快钟：n1=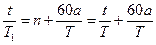
①
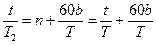对慢钟：n2=
②
联解①②式，并利用单摆周期公式T=2π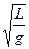
同样可得l=.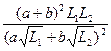
由各摆钟在t s内钟面上显示的时间求解
对快钟：t+60a=
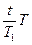①对慢钟：t-60b=
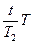②联立解①②式，可得
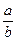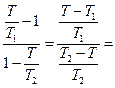
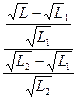
= 最后可得L=
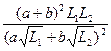.解法二：由各摆钟在t s内的振动次数关系求
设快钟在t s内全振动次数为n1，慢钟为n2，准确的钟为n0.显然，快钟比准确的钟多振动了
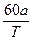次，慢钟比准确的钟少振动了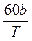次，故：对快钟：n1=
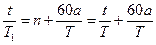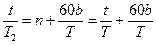①对慢钟：n2=
②联解①②式，并利用单摆周期公式T=2π
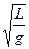
同样可得l=
.
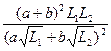练习册系列答案
相关题目
