题目内容
【题目】如图所示，物体小C及长木板B的质量均为m=lkg，B与C通过不可伸长的轻绳跨过光滑的定滑轮连接。设B的右端到定滑轮足够远，C离地面高H=9m，A与B之间的动摩攘因数
=0.2，B与地面的动摩擦因素为
=0.1。B从都止开始释放，同时A(视为质点)在B的左端以v=7m/s的初速度开始运动，且不会从B上掉下，C落地后立即停止运动不反弹，g取10m/s.求：
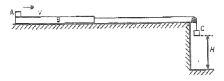
(1)A和B开始运动时的加速度大小；
(2)C落地前的瞬间，轻绳拉力对C做功的功率；
(3)当C落地后，A与B维续运动直至停止，则从A、B、C最开始运动到全部停止的过程中，A与B间的摩擦力对B做的总功为多少?
【答案】（1）
， 
（2）56W （3）
【解析】试题分析：各自受力分析，根据牛顿第二定律即可求出加速度；根据牛顿第二定律求出外力，在由运动学公式求出速度即可求出C落地前的瞬间，轻绳拉力对C做功的功率；根据运动学求出位移再结合功的定义即可求解。
（1）对A根据牛顿第二定律： 
，解得： 
对C： 
对B： 
解得： 
(2) 三者共遠时，时间为东，速度为
： 
解得： 
， 
此时B、C的位移为
之后，对 C： 
对 B： 
解得： 
，T=7N
根据： 
解得：v2=8m/s
功率为：P=T v2=56W
(3) 共速到C落地的时间为
C落地后，对A： 
，解得： 
对 B： 
，解得： 
B共遠时，速度为v3，经历的时间为t3
速度关系为： 
解得： 
， 
，
B的位移为
之后，A、B一起匀减速： 
，解得： 
B的位移为
则全过程A、B间的摩擦力对B所做的功为： 
J
练习册系列答案
相关题目
