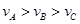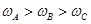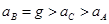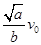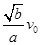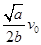题目内容
假如一做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍,仍做匀速圆周运动,则( )
| A.根据公式v=ωr,可知卫星运动的线速度增大到原来的2倍 |
B.根据公式F=G ,可知地球提供的向心力将减小到原来的1/4 ,可知地球提供的向心力将减小到原来的1/4 |
C.根据公式F=m ,可知卫星所需的向心力将减小到原来的1/2 ,可知卫星所需的向心力将减小到原来的1/2 |
D.根据上述选项B和C给出的公式,可知卫星运动的线速度将减小到原来的 /2 /2 |
BD
解析试题分析:人造卫星做圆周运动,万有引力提供向心力,当轨道半径变化时,万有引力变化,卫星的线速度、角速度、周期都随着变化,所以,不能用向心力的表达式来讨论一些物理量的变化,讨论这些物理量时要找准公式,正确使用控制变量法.当轨道半径变化时,万有引力变化,卫星的角速度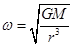 随着变化,所以,不能用公式
随着变化,所以,不能用公式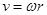 讨论卫星的线速度变化,故A错误;人造卫星的轨道半径增大到原来的2倍,由公式
讨论卫星的线速度变化,故A错误;人造卫星的轨道半径增大到原来的2倍,由公式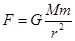 可知地球提供的向心力将减小到原来的
可知地球提供的向心力将减小到原来的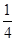 ,故B正确;当轨道半径变化时,万有引力变化,卫星的线速度
,故B正确;当轨道半径变化时,万有引力变化,卫星的线速度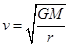 随着变化,所以,不能用公式
随着变化,所以,不能用公式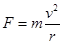 讨论卫星的向心力变化,故C错误;根据万有引力提供向心力,卫星的线速度
讨论卫星的向心力变化,故C错误;根据万有引力提供向心力,卫星的线速度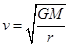 ,可知卫星运动的线速度将减少到原来的
,可知卫星运动的线速度将减少到原来的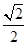 ,故D正确.所以选BD.
,故D正确.所以选BD.
考点:本题考查万有引力定律及其应用,意在考查考生对绕地卫星的线速度与半径、周期、向心力等之间关系的理解和应用能力.

“嫦娥一号”于2009年3月1日下午4时13分成功撞月,从发射到撞月历时433天,标志我国一期探月工程圆满结束.其中,卫星发射过程先在近地圆轨道绕行3周,再长途跋涉进入近月圆轨道绕月飞行.若月球表面的重力加速度为地球表面重力加速度的1/6,月球半径为地球半径的1/4,根据以上信息得( )
A.绕月与绕地飞行周期之比为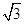 ∶ ∶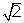 |
B.绕月与绕地飞行周期之比为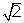 ∶ ∶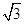 |
| C.绕月与绕地飞行向心加速度之比为6∶1 |
| D.月球与地球质量之比为1∶96 |
已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
A.卫星距地面的高度为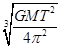 |
| B.卫星的运行速度小于第一宇宙速度 |
C.卫星运行时受到的向心力大小为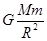 |
| D.卫星运行的向心加速度小于地球表面的重力加速度 |
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。则以下说法正确的是
| A.要将卫星由圆轨道1送入圆轨道3,需要在椭圆轨道2的近地点Q和远地点P分别点火加速一次 |
| B.由于卫星由圆轨道1送入圆轨道3被点火加速两次,则卫星在圆轨道3上正常运行速度要大于在圆轨道1上正常运行的速度 |
| C.卫星在椭圆轨道2上的近地点Q的速度一定大于7.9km/s,而在远地点P的速度一定小于7.9km/s |
| D.卫星在椭圆轨道2上经过P点时的加速度等于它在圆轨道3上经过P点时的加速度 |
根据开普勒对第谷观测记录的研究发现,关于行星的运动,判断下列论述正确的是( )
| A.行星绕太阳做匀速圆周运动 |
| B.在公式R3/T2=k中,k是和太阳的质量有关的量 |
| C.在公式R3/T2=k中,R是行星中心到太阳中心的距离 |
| D.以上三点均不正确 |
我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站。如图所示,关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆轨道的近月点B处与空间站C对接,已知空间站绕月运行的圆轨道的半径为r,周期为T,万有引力常量为G,月球的半径为R.下列说法正确的是: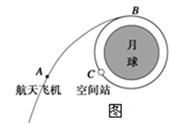
| A.要使对接成功,飞机在接近B点时必须减速 |
| B.航天飞机在图示位置正在加速向B运动 |
| C.月球的质量为M= |
| D.月球的第一宇宙速度为v= |
2012年10月25日,我国将第十六颗北斗卫星“北斗- ”送入太空,并定点于地球静止轨道东经110.5°。由此,具有完全自主知识产权的北斗系统将首先具备为亚太地区提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力。其定位精度优于20m,授时精度优于100ns。关于这颗“北斗-
”送入太空,并定点于地球静止轨道东经110.5°。由此,具有完全自主知识产权的北斗系统将首先具备为亚太地区提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力。其定位精度优于20m,授时精度优于100ns。关于这颗“北斗-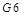 ”卫星以下说法中正确的有 ( )
”卫星以下说法中正确的有 ( )
| A.这颗卫星轨道平面与东经110.5°的经线平面重合 |
| B.通过地面控制可以将这颗卫星定点于成都正上方 |
| C.这颗卫星的线速度大小比离地350公里高的天宫一号空间站线速度要大 |
| D.这颗卫星的周期一定等于地球自转周期,轨道平面一定与赤道平面重合 |
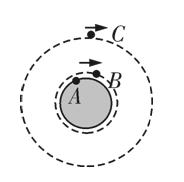
 ,关于它们运行线速度
,关于它们运行线速度 、角速度
、角速度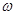 、周期
、周期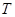 和加速度
和加速度 的比较正确的是( )
的比较正确的是( )