题目内容
已知地球质量为M，半径为R，自转周期为T，地球同步卫星质量为m，引力常量为G，有关同步卫星，下列表述正确的是( )
A．卫星距地面的高度为 |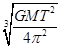
| B．卫星的运行速度小于第一宇宙速度 |
C．卫星运行时受到的向心力大小为 |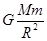
| D．卫星运行的向心加速度小于地球表面的重力加速度 |
BD
解析试题分析：设同步卫星离地面的高度为h，由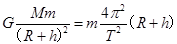
，得
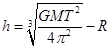；由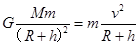
，得卫星的运行速度
；同步卫星所需要的向心力是由地球对其的万有引力提供，即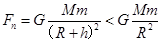
；卫星运行的向心加速度
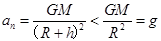，所以正确选项为B、D。
考点：本题考查了万有引力定律及应用。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案如图所示，一颗行星和一颗彗星绕同一恒星的运行轨道分别为A和B，A是半径为r的圆轨道，B为椭圆轨道，椭圆长轴QQ′为2r。P点为两轨道的交点，以下说法正确的是
| A．彗星和行星经过P点时受到的万有引力相等 |
| B．彗星和行星绕恒星运动的周期相同 |
| C．彗星和行星经过P点时的速度相同 |
| D．彗星在Q′处加速度为行星加速度的1/4 |
我国研制并成功发射的“嫦娥二号”探测卫星，在距月球表面高度为h的轨道上做匀速圆周运动，运行的周期为T。若以R表示月球的半径，则( )
A．卫星运行时的向心加速度为 |
B．卫星运行时的线速度为 |
| C．物体在月球表面自由下落的加速度为 |
D．月球的第一宇宙速度为 |
我国射的“神舟八号”飞船与先期发射的“天宫一号”空间站实现了完美对接。已知“天宫一号”绕地球做圆轨道运动，轨道半径为r，周期为T，万有引力常量为G。假设沿椭圆轨道运动的“神州八号”环绕地球的运动方向与“天宫一号”相同，远地点与“天宫一号”的圆轨道相切于某点P，并在该点附近实现对接，如图所示。则下列说法正确的是：（ ）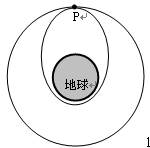
| A．根据题设条件可以计算出地球对“天宫一号”的引力大小 |
| B．在远地点P处，“神舟八号”的加速度比“天宫一号”大 |
| C．根据题中条件可以计算出地球的质量 |
| D．要实现在远地点P处对接，“神舟八号”需在靠近P处之前应该点火减速 |
我国已成功发射多颗卫星，为实现国人的飞天梦想提供了大量的信息、科技支持。嫦娥一号的成功发射，标志着我国新的航天时代的到来。已知发射的卫星中，卫星A是极地圆形轨道卫星，卫星B是地球同步卫星，二者质量相同，且卫星A的运行周期是卫星B的一半。根据以上相关信息，比较这两颗卫星，下列说法中正确的是（ ）
| A．卫星B离地面较近，卫星A离地面较远 |
| B．正常运行时卫星A的线速率比卫星B的线速率大 |
| C．卫星A和卫星B由西昌卫星发射中心发射时卫星A比卫星B的发射难度大 |
| D．卫星A对地球的观测范围比卫星B的观测范围大 |
，神舟飞船在地球表面附近的圆形轨道运行周期为
，火星质量与地球质量之比为p，火星半径与地球半径之比为q，则
假如一做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍，仍做匀速圆周运动，则（ ）
| A．根据公式v＝ωr，可知卫星运动的线速度增大到原来的2倍 |
B．根据公式F＝G ，可知地球提供的向心力将减小到原来的1/4 |
C．根据公式F＝m ，可知卫星所需的向心力将减小到原来的1/2 |
D．根据上述选项B和C给出的公式，可知卫星运动的线速度将减小到原来的 /2 |
“天宫一号”和“神舟八号”绕地球做匀速圆周运动的示意图如图所示，A代表“天宫一号”，B代表“神舟八号”，虚线为各自的轨道。可以判定( )
| A．“天宫一号”的运行速率大于“神舟八号”的运行速率 |
| B．“天宫一号”的周期小于“神舟八号”的周期 |
| C．“天宫一号”的向心加速度大于“神舟八号”的向心加速度 |
| D．“神舟八号”适度加速有可能与“天宫一号”实现对接 |
