Question

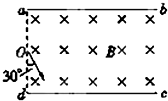
如图所示，质量为m、电荷量为q的带电粒子，经电势差为U的电场加速后，从O点垂直MN边界进入磁感应强度大小为B、方向垂直纸面向外的匀强磁场中，速度方向与磁场方向垂直，最后在MN边界上的P点．设带电粒子初速度为零且不计重力，求：
（1）粒子带何种电荷及粒子进入磁场时的速率；
（2）OP间的距离．

Answer 1

（1）带电粒子在电场中受力运动的方向是从正极向负极，可以判定电荷该粒子带正电；
粒子在电场中被加速．由动能定理得：qU=

1

2

mv²-0，
解得：v=

2qU m

；
（2）粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律可得：
qvB=m

v2

r

，
解得：r=

1

B

2mU q

，
OP间的距离：OP=2r=

2

B

2mU q

；
答：（1）粒子带正电荷，粒子进入磁场时的速率为

2qU m

；
（2）OP间的距离为

2

B

2mU q

．