题目内容
钍核
Th发生衰变生成镭核
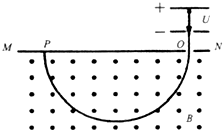
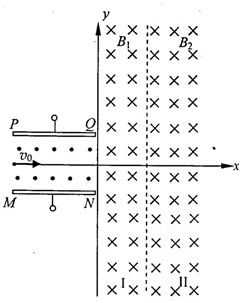
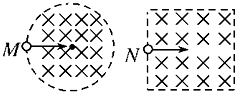
Ra并放出一个粒子.设该粒子的质量为m、电荷量为q,它刚进入电势差为U的带狭缝的平行板电极S1和S2间电场时速度为v0,经电场加速后,沿Ox方向进入磁感应强度为B、方向垂直于纸面向外的匀强磁场中,如图所示,整个装置处于真空中.
(1)写出钍核衰变的方程;
(2)粒子从S2狭缝射出来时的速度v多大?
(3)粒子在磁场中做圆周运动的轨道半径R多大?

| 23090 |
| 22688 |
(1)写出钍核衰变的方程;
(2)粒子从S2狭缝射出来时的速度v多大?
(3)粒子在磁场中做圆周运动的轨道半径R多大?

(1)由质量数与核电荷数守恒可知,
核反应方程为:
Th→
Ra+
He;
(2)在加速电场中,由动能定理得:
qU=
mv2-
mv02,解得:v=
;
(3)粒子在匀强磁场中做匀速圆周运动,
由牛顿第二定律得:qvB=m
,
解得:R=
;
答:(1)钍核衰变的方程为:
Th→
Ra+
He;(2)粒子从S2狭缝射出来时的速度为
;(3)粒子在磁场中做圆周运动的轨道半径为:
.
核反应方程为:
| 23090 |
| 22688 |
| 42 |
(2)在加速电场中,由动能定理得:
qU=
| 1 |
| 2 |
| 1 |
| 2 |
|
(3)粒子在匀强磁场中做匀速圆周运动,
由牛顿第二定律得:qvB=m
| v2 |
| R |
解得:R=
| m |
| qB |
|
答:(1)钍核衰变的方程为:
| 23090 |
| 22688 |
| 42 |
|
| m |
| qB |
|

练习册系列答案
相关题目