题目内容
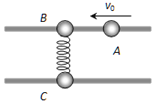
【题目】在相互平行且足够长的两根水平光滑的硬杆上,穿着三个半径相同的刚性球A、B、C,三球的质量分别为
、
、
,初状态BC球之间连着一根轻质弹簧并处于静止,B、C连线与杆垂直并且弹簧刚好处于原长状态,A球以
的速度向左运动,与同一杆上的B球发生完全非弹性碰撞
碰撞时间极短
,求：
球与B球碰撞过程中损耗的机械能；
在以后的运动过程中弹簧的最大弹性势能；
【答案】(1)27J(2)9J
【解析】
(1) A、B发生完全非弹性碰撞，以向左为正方向，根据动量守恒定律有：
mAv0=（mA+mB）v1
代入数据解得，碰后A、B的共同速度：
v1=3m/s
损失的机械能为：
(2) A、B、C系统动量守恒、机械能守恒，三者速度相等时弹簧弹性势能最大，以向左为正方向，由动量守恒定律得：
（mA+mB）v1=（mA+mB+mC）v2
代入数据解得：
v2=1m/s
弹簧最大弹性势能：
代入数据解得：
Epm=9J
练习册系列答案
阅读快车系列答案
相关题目
