题目内容
如图所示,在竖直平面内固定着半径为R的半圆形轨道,小球B静止在轨道的最低点,小球A从轨道右端正上方3.5R处由静止自由落下,沿圆弧切线进入轨道后,与小球B发生弹性碰撞.碰撞后B球上升的最高点C,圆心O与C的连线与竖直方向的夹角为60°.若两球均可视为质点,不计一切摩擦,求A、B两球的质量之比mA:mB.
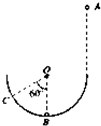

小球A从高处静止下落至轨道的最低点,
由机械能守恒定律得:mAg?(3.5R+R)=
mAv02,
小球A与小球B发生弹性碰撞,动量守恒,机械能守恒,
以A、B两球组成的系统为研究对象,以A的初速度方向为正方向,
由动量守恒定律得:mAv0=mAvA+mBvB,
由机械能守恒定律得:
mAv02=
mAvA2+
mBvB2,
B球上升到最高点C,机械能守恒,
由机械能守恒定律得:
mBvB2=mBgR(1-cos60°),
解得:mA:mB=1:5.
答:A、B两球的质量之比为1:5.
由机械能守恒定律得:mAg?(3.5R+R)=
| 1 |
| 2 |
小球A与小球B发生弹性碰撞,动量守恒,机械能守恒,
以A、B两球组成的系统为研究对象,以A的初速度方向为正方向,
由动量守恒定律得:mAv0=mAvA+mBvB,
由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
B球上升到最高点C,机械能守恒,
由机械能守恒定律得:
| 1 |
| 2 |
解得:mA:mB=1:5.
答:A、B两球的质量之比为1:5.

练习册系列答案
相关题目
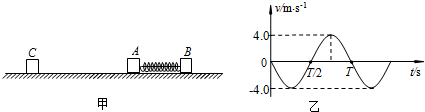 时,物体A的速度?时间图象如图乙所示.求:
时,物体A的速度?时间图象如图乙所示.求:



