题目内容
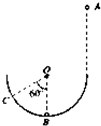
如图所示,一个质量为m的木块,从半径为R、质量为M的
光滑圆槽顶端由静止滑下.在槽被固定和可沿着光滑平面自由滑动两种情况下,木块从槽口滑出时的速度大小之比为多少?

| 1 |
| 4 |

圆槽固定时,木块下滑过程中只有重力做功,
由动能定理得:mgR=
mv
-0…①
解得:木块滑出槽口时的速度:v1=
…②
圆槽可动时,当木块开始下滑到脱离槽口的过程中,
对木块和槽所组成的系统,水平方向不受外力,
水平方向动量守恒,设木块滑出槽口时的速度为v2,槽的速度为u,
在水平方向上,由动量守恒定律可得:mv2-Mu=0…③
木块下滑时,只有重力做功,系统机械能守恒,
由机械能守恒定律得:mgR=
mv
+
Mu2…④
由③④解得,木块滑出槽口的速度:v2=
…⑤
两种情况下滑出槽口的速度之比:
=
=
;
答:两种情况下,木块从槽口滑出时的速度大小之比为
.
由动能定理得:mgR=
| 1 |
| 2 |
| 21 |
解得:木块滑出槽口时的速度:v1=
| 2gR |
圆槽可动时,当木块开始下滑到脱离槽口的过程中,
对木块和槽所组成的系统,水平方向不受外力,
水平方向动量守恒,设木块滑出槽口时的速度为v2,槽的速度为u,
在水平方向上,由动量守恒定律可得:mv2-Mu=0…③
木块下滑时,只有重力做功,系统机械能守恒,
由机械能守恒定律得:mgR=
| 1 |
| 2 |
| 22 |
| 1 |
| 2 |
由③④解得,木块滑出槽口的速度:v2=
|
两种情况下滑出槽口的速度之比:
| v1 |
| v2 |
| ||
|
|
答:两种情况下,木块从槽口滑出时的速度大小之比为
|

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目