��Ŀ����
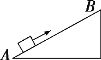
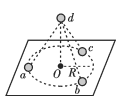
����Ŀ����ͼ��ʾ�����Ϊһ���̶���ˮƽ�����ϵİ뾶ΪR=1m�İ���������������ֱ��ABˮƽ��O��Ϊ���ģ�����ڱ��漰�����ڹ⻬���Ҳ���һ���㹻���Ĺ̶��⻬б�桢б�����Ϊ45����һ�������쳤������ϸ����������ڼ���ֱ�̶������ʹ⻬�����֣�ϸ�����˷ֱ�ϵ�п���Ϊ�ʵ��С��m1�����m2����m1=m2=2kg����ʼʱm1ǡ��A�㣬m2��б�����Ҿ��붥���㹻Զ����ʱ����m1��m2��ϸ����б��ƽ����ǡ����ֱ��C����Բ��O�����·�����m1�ɾ�ֹ�ͷſ�ʼ�˶���������˵������ȷ���ǣ�������
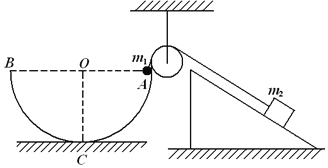
A. m1�˶���C��ʱ������� B. ��m1�˶���C��ʱ��m2������2m/s
C. m1�˶���C��ʱ������Ϊ16N D. m1������������������B��
���𰸡�BCD
��������
A����m1��A���˶���C��Ĺ����У�m1��m2��ɵ�ϵͳֻ������������ϵͳ�Ļ�е���غ㡣��A��ȷ��
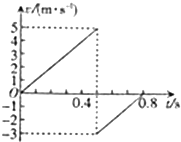
B����С��m1������͵�Cʱm1��m2���ٶȴ�С�ֱ�Ϊv1��v2�����˶��ĺϳɷֽ�ã�v1cos45��=v2����![]() ����m1�˶�����͵�ʱ��AB��ɵ�ϵͳ�����ݶ��ܶ�����֪
����m1�˶�����͵�ʱ��AB��ɵ�ϵͳ�����ݶ��ܶ�����֪![]() �����v2=2m/s��
�����v2=2m/s��![]() m/s����B��ȷ��
m/s����B��ȷ��
C����C�㣬����F=![]() ��֪F=
��֪F=![]() ����C��ȷ��
����C��ȷ��
D����m1��A���˶���C��Ĺ����У���m1��m2��ɵ�ϵͳ�ɻ�е���غ㶨�ɵã�![]() �����
�����![]() ��ã�v1��
��ã�v1��![]()
��m1�˶���C��ʱ���Ͽ���������Ҫ��![]() ���ٶ�m1����������������B�㣬������m1�����Ĺ��������Ӷ���������������m1������������������B�㡣��D��ȷ��
���ٶ�m1����������������B�㣬������m1�����Ĺ��������Ӷ���������������m1������������������B�㡣��D��ȷ��
��ѡBCD��