题目内容
12.如果将地球看作是一个均匀的球体,半径为R=6400km,在地球赤道表面上的物体A随地球自转的线速度是多少?在北纬30°的物体B随地球自转的线速度是多少?分析 地球自转的周期为24h,根据ω=$\frac{2π}{T}$求出地球自转的角速度;通过地球的半径,根据v=Rω求出赤道上的物体自转具有的线速度.
解答 解:地球自转的周期为24h,则自转的角速度为:
ω=$\frac{2π}{T}$=$\frac{2π}{24×3600}≈7.27×1{0}^{-5}rad/s$;
赤道上物体自转具有的线速度为:
v=Rω=6400×103×7.27×10-5m/s=465.2m/s.
根据几何关系可知:人随地球转动的半径为:Rcos30°
所以有:v=ωRcos30°=7.27×10-5rad/s×6.4×106×$\frac{\sqrt{3}}{2}$=402m/s;
答:地球赤道表面上的物体A随地球自转的线速度是465.2m/s;
在北纬30°的物体B随地球自转的线速度是402m/s.
点评 本题主要考查了线速度与角速度的关系及周期与角速度之间的关系,要知道站在地球上的人与地球具有相同的角速度,难度不大,但要注意单位的统一.

练习册系列答案
相关题目
2. 如图所示,相距为d的边界水平的匀强磁场,磁感应强度垂直纸面向里、大小为B.质量为m、电阻为R、边长为L的正方形线圈M,将线圈在磁场上方高h处由静止释放,已知cd边刚进入磁场时和cd边刚离开磁场时速度相等,不计空气阻力,则( )
如图所示,相距为d的边界水平的匀强磁场,磁感应强度垂直纸面向里、大小为B.质量为m、电阻为R、边长为L的正方形线圈M,将线圈在磁场上方高h处由静止释放,已知cd边刚进入磁场时和cd边刚离开磁场时速度相等,不计空气阻力,则( )
 如图所示,相距为d的边界水平的匀强磁场,磁感应强度垂直纸面向里、大小为B.质量为m、电阻为R、边长为L的正方形线圈M,将线圈在磁场上方高h处由静止释放,已知cd边刚进入磁场时和cd边刚离开磁场时速度相等,不计空气阻力,则( )
如图所示,相距为d的边界水平的匀强磁场,磁感应强度垂直纸面向里、大小为B.质量为m、电阻为R、边长为L的正方形线圈M,将线圈在磁场上方高h处由静止释放,已知cd边刚进入磁场时和cd边刚离开磁场时速度相等,不计空气阻力,则( )| A. | 若L=d,则线圈穿过磁场的整个过程用时为$\sqrt{\frac{2}{gh}d}$ | |
| B. | 在线圈穿过磁场的整个过程中,克服安培力做功为mgd | |
| C. | 若L<d则线圈穿过磁场的整个过程中最小速度可能$\frac{mgR}{{{B^2}{L^2}}}$ | |
| D. | 若L<d,则线圈穿过磁场的整个过程中最小速度可能$\sqrt{2g(h+L-d)}$ |
7. 如图所示,水平面上是高AC=H、倾角为30°的直角三角形斜面,长2H、质量为m的均匀细绳一端栓有质量为m且可看作质点的小球,另一端在外力F作用下从A点开始缓慢运动到B点,不计一切摩擦以及绳绷紧时的能量损失,则该过程中( )
如图所示,水平面上是高AC=H、倾角为30°的直角三角形斜面,长2H、质量为m的均匀细绳一端栓有质量为m且可看作质点的小球,另一端在外力F作用下从A点开始缓慢运动到B点,不计一切摩擦以及绳绷紧时的能量损失,则该过程中( )
 如图所示,水平面上是高AC=H、倾角为30°的直角三角形斜面,长2H、质量为m的均匀细绳一端栓有质量为m且可看作质点的小球,另一端在外力F作用下从A点开始缓慢运动到B点,不计一切摩擦以及绳绷紧时的能量损失,则该过程中( )
如图所示,水平面上是高AC=H、倾角为30°的直角三角形斜面,长2H、质量为m的均匀细绳一端栓有质量为m且可看作质点的小球,另一端在外力F作用下从A点开始缓慢运动到B点,不计一切摩擦以及绳绷紧时的能量损失,则该过程中( )| A. | 重力对绳做功为0 | B. | 绳重力势能增加了$\frac{5}{4}$mgH | ||
| C. | 绳的机械能增加了$\frac{1}{4}$mgH | D. | 小球对绳的拉力做功$\frac{1}{4}$mgH |
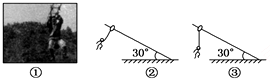
2.如图①所示,高空滑索是一种勇敢者的运动项目.如果一个人用轻绳通过轻质滑环悬吊在足够长的倾斜钢索上运动,在下滑过程中可能会出现如图②(绳与钢索垂直)和如图③(绳竖直)所示的两种情形.不计空气阻力,则下列说法正确的是( )

| A. | 图②的情形中,钢索对轻环的作用力大小为2mg | |
| B. | 图②的情形中,人只能匀加速下滑 | |
| C. | 图③的情形中,人匀加速下滑 | |
| D. | 图③的情形中,钢索对轻环无摩擦力 |
6. 如图所示,直角坐标系xOy位于竖直平面内.第Ⅲ、IV象限内有垂直于坐标面向外的匀强磁场,第IV象限同时存在方向平行于y轴的匀强电场(图中未画出),一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进人第IV象限,然后做圆周运动,从Q点垂直于x轴进入第I象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,不能求出的物理量有( )
如图所示,直角坐标系xOy位于竖直平面内.第Ⅲ、IV象限内有垂直于坐标面向外的匀强磁场,第IV象限同时存在方向平行于y轴的匀强电场(图中未画出),一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进人第IV象限,然后做圆周运动,从Q点垂直于x轴进入第I象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,不能求出的物理量有( )
 如图所示,直角坐标系xOy位于竖直平面内.第Ⅲ、IV象限内有垂直于坐标面向外的匀强磁场,第IV象限同时存在方向平行于y轴的匀强电场(图中未画出),一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进人第IV象限,然后做圆周运动,从Q点垂直于x轴进入第I象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,不能求出的物理量有( )
如图所示,直角坐标系xOy位于竖直平面内.第Ⅲ、IV象限内有垂直于坐标面向外的匀强磁场,第IV象限同时存在方向平行于y轴的匀强电场(图中未画出),一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进人第IV象限,然后做圆周运动,从Q点垂直于x轴进入第I象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,不能求出的物理量有( )| A. | 圆周运动的速度大小 | B. | 电场强度的大小和方向 | ||
| C. | 小球在第IV象限运动的时间 | D. | 磁感应强度大小 |
7. 如图,半径为R的圆是圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B.方向垂直纸面向外,一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为$\frac{R}{2}$.已知粒子射出磁场与射入磁场时运动方向间的夹角为90°,则粒子的速率为(不计重力)( )
如图,半径为R的圆是圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B.方向垂直纸面向外,一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为$\frac{R}{2}$.已知粒子射出磁场与射入磁场时运动方向间的夹角为90°,则粒子的速率为(不计重力)( )
 如图,半径为R的圆是圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B.方向垂直纸面向外,一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为$\frac{R}{2}$.已知粒子射出磁场与射入磁场时运动方向间的夹角为90°,则粒子的速率为(不计重力)( )
如图,半径为R的圆是圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B.方向垂直纸面向外,一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为$\frac{R}{2}$.已知粒子射出磁场与射入磁场时运动方向间的夹角为90°,则粒子的速率为(不计重力)( )| A. | $\frac{qBR}{2m}$ | B. | $\frac{(\sqrt{3}-1)qBR}{2m}$ | C. | $\frac{qBR}{m}$ | D. | $\frac{(\sqrt{3}+1)qBR}{2m}$ |
 如图所示,用钳子夹住一块质量m=50kg的混凝土砌块起吊,已知钳子与砌块间的动摩擦因数μ=0.4,砌块重心至上端间距L=4m,当钳子沿水平方向以速度v=4m/s匀速运动时上端突然停止,为了不使砌块从钳子口滑下,问:此时钳子对砌块施加的水平压力N至少为多大?(认为最大静摩擦力与滑动摩擦力大小相等)
如图所示,用钳子夹住一块质量m=50kg的混凝土砌块起吊,已知钳子与砌块间的动摩擦因数μ=0.4,砌块重心至上端间距L=4m,当钳子沿水平方向以速度v=4m/s匀速运动时上端突然停止,为了不使砌块从钳子口滑下,问:此时钳子对砌块施加的水平压力N至少为多大?(认为最大静摩擦力与滑动摩擦力大小相等) 如图,已知一斜面倾角是30°,其高度是1m,将一个10kg的物体放在斜面顶端,物体恰好匀速下滑.求:
如图,已知一斜面倾角是30°,其高度是1m,将一个10kg的物体放在斜面顶端,物体恰好匀速下滑.求: 如图所示,一定质量的理想气体经历A→B、B→C、C→A三个变化过程,则:
如图所示,一定质量的理想气体经历A→B、B→C、C→A三个变化过程,则: