题目内容
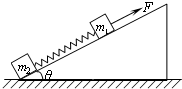 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则
- A.弹簧的弹力为
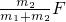
- B.弹簧的弹力为
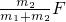 +μm2gsinθ
+μm2gsinθ - C.地面对斜面的摩擦力水平向左
- D.地面对斜面的摩擦力水平向右
AC
分析:由题,m1、m2一起向上作匀加速运动,先根据牛顿第二定律求出加速度,再对m1研究,由牛顿第二定律求出弹簧的弹力.以斜面为研究对象,由平衡条件分析地面对斜面的摩擦力方向.
解答:A、B根据牛顿第二定律得:
对m1、m2整体:F-μ(m1+m2)gcosθ-(m1+m2)gsinθ=(m1+m2)a,
对m1:F弹-μm1gcosθ-m1gsinθ=m1a,
联立上两式得:F弹=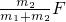 .故A正确,B错误.
.故A正确,B错误.
C、D以斜面为研究对象,分析受力情况:重力G、m1、m2的压力N1和滑动摩擦力f1、地面的支持力N2,如图,则由平衡条件可知,地面对斜面的摩擦力f2必定水平向左,斜面才能保持平衡.故C正确,D错误.
故选AC
点评:本题解题关键是研究对象的选择,采用整体法和隔离法相结合的方法求解弹簧的弹力,运用隔离法分析,地面对斜面的摩擦力的方向.
分析:由题,m1、m2一起向上作匀加速运动,先根据牛顿第二定律求出加速度,再对m1研究,由牛顿第二定律求出弹簧的弹力.以斜面为研究对象,由平衡条件分析地面对斜面的摩擦力方向.
解答:A、B根据牛顿第二定律得:

对m1、m2整体:F-μ(m1+m2)gcosθ-(m1+m2)gsinθ=(m1+m2)a,
对m1:F弹-μm1gcosθ-m1gsinθ=m1a,
联立上两式得:F弹=
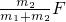 .故A正确,B错误.
.故A正确,B错误.C、D以斜面为研究对象,分析受力情况:重力G、m1、m2的压力N1和滑动摩擦力f1、地面的支持力N2,如图,则由平衡条件可知,地面对斜面的摩擦力f2必定水平向左,斜面才能保持平衡.故C正确,D错误.
故选AC
点评:本题解题关键是研究对象的选择,采用整体法和隔离法相结合的方法求解弹簧的弹力,运用隔离法分析,地面对斜面的摩擦力的方向.

练习册系列答案
相关题目
 如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1、μB=0.2,取g=10m/s2.
如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1、μB=0.2,取g=10m/s2. 如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在大小相等的两力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),斜向上的力F与水平方向成θ角,轻弹簧与水平方向成α角.则m1所受支持力FN、摩擦力f和弹簧弹力T正确的是( )
如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在大小相等的两力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),斜向上的力F与水平方向成θ角,轻弹簧与水平方向成α角.则m1所受支持力FN、摩擦力f和弹簧弹力T正确的是( ) 如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( )
如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( ) 如图所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上,整个直杆被固定于竖直转轴上,并保持水平,两球间用劲度系数为K,自然长度为L的轻质弹簧连接在一起,左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L,现欲使横杆P随竖直转轴一起在水平面内匀速转动,其角速度为ω,求当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少?
如图所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上,整个直杆被固定于竖直转轴上,并保持水平,两球间用劲度系数为K,自然长度为L的轻质弹簧连接在一起,左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L,现欲使横杆P随竖直转轴一起在水平面内匀速转动,其角速度为ω,求当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少? 如图所示,质量分别为mA、mB的A、B两物体置于动摩擦因数为μ的粗糙水平面上,它们之间用轻质弹簧连接,在A上施加一个水平向右的恒力F,两物块一起以加速度a向右做匀加速运动,此时弹簧伸长量为x;若将力的大小增大到F'=2F时,两物块均以加速度a'做匀加速运动,此时弹簧伸长量为x',则( )
如图所示,质量分别为mA、mB的A、B两物体置于动摩擦因数为μ的粗糙水平面上,它们之间用轻质弹簧连接,在A上施加一个水平向右的恒力F,两物块一起以加速度a向右做匀加速运动,此时弹簧伸长量为x;若将力的大小增大到F'=2F时,两物块均以加速度a'做匀加速运动,此时弹簧伸长量为x',则( )