题目内容
8. 如图所示,在一厚度为d,折射率为n的大玻璃板的下表面,有一半径为r的圆形发光面,已知真空中的光速为c;
如图所示,在一厚度为d,折射率为n的大玻璃板的下表面,有一半径为r的圆形发光面,已知真空中的光速为c;①从玻璃板上表面射出的光在玻璃中传播的最短时间tmin
②为了从玻璃的上方看不见圆形发光面,在玻璃板的上表面贴有一块不透光的圆形纸片,求贴圆形纸片的最小面积Smin.
分析 ①光在玻璃中的速度是固定的,故位移最小时传播时间最短,故光线与边界垂直时用时最短;
②作出光路图,取圆形发光面边缘上一点,由该点发出的光线能射出玻璃板的范围由临界光线确定,当入射角大于临界角C时,光线就不能射出玻璃板了,根据折射定律和几何知识结合进行求解.
解答 解:①当光垂直于玻璃板的上下表面时,其在玻璃中传播的时间最短,有:
tmin=$\frac{d}{min}$,其中v=$\frac{c}{n}$,
解得:tmin=$\frac{nd}{c}$;
②设E为圆形发光面边缘上的一点,若由该点发出的光线恰好在玻璃的上表面发生全反射,则此光线的入射角等于临界角,如图所示,由几何关系有:△r=d•tanC,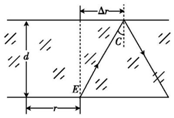
又:sinC=$\frac{1}{n}$,
解得:△r=$\frac{d}{\sqrt{{n}^{2}-1}}$,
故所贴圆形纸片的最小半径为:R=r+△r,
又:Smin=πR2,
解得:Smin=π(r+$\frac{d}{\sqrt{{n}^{2}-1}}$)2.
答:①从玻璃板上表面射出的光在玻璃中传播的最短时间tmin为$\frac{nd}{c}$;
②贴圆形纸片的最小面积Smin为π(r+$\frac{d}{\sqrt{{n}^{2}-1}}$)2.
点评 本题关键要理解看不到圆形发光面的原因是由于发生了全反射,再作出光路图,运用折射定律和几何知识结合进行求解.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
18. 一列简谐横波沿x轴传播.t=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )
一列简谐横波沿x轴传播.t=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )
 一列简谐横波沿x轴传播.t=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )
一列简谐横波沿x轴传播.t=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )| A. | 此波沿x轴正方向传播 | |
| B. | 此波的传播速度为25m/s | |
| C. | 从t=0时起,经过0.04s,质点A沿波传播方向迁移了1m | |
| D. | 在t=0.04s时,质点B处在平衡位置,速度沿y轴正方向 | |
| E. | 此列波不能和频率为50 Hz的横波发生干涉现象 |
19.一个质量为m1的人造地球卫星在高空做匀速圆周运动,轨道半径为r.某时刻和一个质量为m2的同轨道反向运动的太空碎片发生迎面正碰,碰后二者结合成一个整体,并开始沿椭圆轨道运动,轨道的远地点为碰撞时的点.若碰后卫星的内部装置仍能有效运转,当卫星与碎片的整体再次经过远地点时,通过极短时间喷气可使整体仍在卫星碰前的轨道上做圆周运动,绕行方向与碰前相同.已知地球的半径为R,地球表面的重力加速度大小为g,下列说法正确的是( )
| A. | 卫星与碎片碰撞前的线速度大小为$\frac{{gR}^{2}}{r}$ | |
| B. | 卫星与碎片碰撞前运行的周期大小为$\frac{2πr}{R}\sqrt{\frac{r}{g}}$ | |
| C. | 喷气装置对卫星和碎片整体所做的功为$\frac{{{{2m}_{1}m}_{2}gR}^{2}}{{{(m}_{1}+m}_{2})r}$ | |
| D. | 喷气装置对卫星和碎片整体所做的功为$\frac{{{{m}_{1}m}_{2}gR}^{2}}{{{(m}_{1}+m}_{2})r}$ |
16. 如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v甲、v乙沿水平方向抛出甲、乙两个小球,甲球落在C点、乙球落在D点,OC、OD与竖直方向的夹角均为30°.下列结论正确的是( )
如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v甲、v乙沿水平方向抛出甲、乙两个小球,甲球落在C点、乙球落在D点,OC、OD与竖直方向的夹角均为30°.下列结论正确的是( )
 如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v甲、v乙沿水平方向抛出甲、乙两个小球,甲球落在C点、乙球落在D点,OC、OD与竖直方向的夹角均为30°.下列结论正确的是( )
如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v甲、v乙沿水平方向抛出甲、乙两个小球,甲球落在C点、乙球落在D点,OC、OD与竖直方向的夹角均为30°.下列结论正确的是( )| A. | 甲、乙两球运动时间不等 | |
| B. | 甲、乙两球下落过程中速度变化量相同 | |
| C. | v甲:v乙=1:2 | |
| D. | v甲:v乙=l:3 |
20. 如图,直线边界ac的下方有垂直于纸面向外的匀强磁场,磁感应强度大小为B.边长为L的正三角形导线框(粗细均匀)绕过a点的转轴在纸面内顺时针匀速转动,角速度为ω.当ac边刚进人磁场时,a、c两点间的电压为( )
如图,直线边界ac的下方有垂直于纸面向外的匀强磁场,磁感应强度大小为B.边长为L的正三角形导线框(粗细均匀)绕过a点的转轴在纸面内顺时针匀速转动,角速度为ω.当ac边刚进人磁场时,a、c两点间的电压为( )
 如图,直线边界ac的下方有垂直于纸面向外的匀强磁场,磁感应强度大小为B.边长为L的正三角形导线框(粗细均匀)绕过a点的转轴在纸面内顺时针匀速转动,角速度为ω.当ac边刚进人磁场时,a、c两点间的电压为( )
如图,直线边界ac的下方有垂直于纸面向外的匀强磁场,磁感应强度大小为B.边长为L的正三角形导线框(粗细均匀)绕过a点的转轴在纸面内顺时针匀速转动,角速度为ω.当ac边刚进人磁场时,a、c两点间的电压为( )| A. | $\frac{1}{6}$BωL2 | B. | $\frac{1}{3}$BωL2 | C. | $\frac{2}{3}$BωL2 | D. | BωL2 |
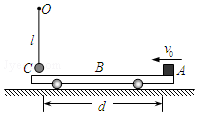 如图所示,一质量为m的小球C用轻绳悬挂在O点,小球下方有一质量为2m的平板车B静止在光滑水平地面上,小球的位置比车板略高,一质量为m的物块A以大小为v0的初速度向左滑上平板车,此时A、C间的距离为d,一段时间后,物块A与小球C发生碰撞,碰撞时两者的速度互换,且碰撞时间极短,已知物块与平板车间的动摩擦因数为μ,重力加速度为g,若A碰C之前物块与平板车已达共同速度,求:
如图所示,一质量为m的小球C用轻绳悬挂在O点,小球下方有一质量为2m的平板车B静止在光滑水平地面上,小球的位置比车板略高,一质量为m的物块A以大小为v0的初速度向左滑上平板车,此时A、C间的距离为d,一段时间后,物块A与小球C发生碰撞,碰撞时两者的速度互换,且碰撞时间极短,已知物块与平板车间的动摩擦因数为μ,重力加速度为g,若A碰C之前物块与平板车已达共同速度,求:
 ,此时恰好由一辆自行车(可视为质点)从火车头旁边同方向驶过,自行车速度
,此时恰好由一辆自行车(可视为质点)从火车头旁边同方向驶过,自行车速度 ,火车长
,火车长 。求:
。求: 如图所示,在与水平方向成53°的斜向上F=32N的拉力作用下,质量为4kg的小物块从静止开始沿水平地面做匀加速直线运动,前进6m时撤掉F,小物块运动一段距离后停止,已知物块与地面之间的动摩擦因数μ=0.5,sin53°=0.8,cos53°=0.6,g=10m/s2,求:
如图所示,在与水平方向成53°的斜向上F=32N的拉力作用下,质量为4kg的小物块从静止开始沿水平地面做匀加速直线运动,前进6m时撤掉F,小物块运动一段距离后停止,已知物块与地面之间的动摩擦因数μ=0.5,sin53°=0.8,cos53°=0.6,g=10m/s2,求: