题目内容
如图所示,是某次发射人造卫星的示意图,人造卫星先在近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上的速度为v1,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上的速度为v3,则以上各速度的大小关系是( )
| A.v1>v2a>v2b>v3 |
| B.v1<v2a<v2b<v3 |
| C.v2a>v1>v3>v2b |
| D.v2a>v1>v2b>v3 |
C
解析试题分析:卫星在轨道1和轨道3上做匀速圆周运动,万有引力提供向心力,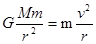 ,所以有:
,所以有:  ,轨道半径越小,卫星的速度越大,则有v1>v3.卫星在轨道2上做椭圆运动,根据开普勒定律得知,v2a>v2b.卫星从轨道1变轨到轨道2,在a点加速,则有v2a>v1.卫星从轨道2变轨到轨道3,在b点加速,则有v3>v2b.所以v2a>v1>v3>v2b,C正确。
,轨道半径越小,卫星的速度越大,则有v1>v3.卫星在轨道2上做椭圆运动,根据开普勒定律得知,v2a>v2b.卫星从轨道1变轨到轨道2,在a点加速,则有v2a>v1.卫星从轨道2变轨到轨道3,在b点加速,则有v3>v2b.所以v2a>v1>v3>v2b,C正确。
考点:本题考查了万有引力定律和卫星问题。

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案如图所示,直径为d的纸筒绕垂直于纸面的O轴匀速转动(图示为截面).从枪口射出的子弹以速度v沿直径穿过圆筒,若子弹穿过圆筒时先后在筒上留下a、b两个弹孔.则圆筒转动的角速度ω可能为( )
A. | B. | C. | D. |
如图所示,一个内壁光滑的圆锥筒,其轴线垂直于水平面,圆锥筒固定不动。有一质量为m的小球A紧贴着筒内壁在水平面内做匀速圆周运动,筒口半径和筒高分别为R和H,小球A所在的高度为筒高的一半。已知重力加速度为 ,则
,则
A.小球A做匀速圆周运动的角速度 |
| B.小球A受到重力、支持力和向心力三个力作用 |
C.小球A受到的合力大小为 |
| D.小球A受到的合力方向垂直筒壁斜向上 |
我国发射的“天宫一号”目标飞行器与发射的“神舟八号”飞船成功进行了第一次无人交会对接.假设对接前“天宫一号”和“神舟八号”绕地球做匀速圆周运动的轨道如图所示,虚线A代表“天宫一号”的轨道,虚线B代表“神舟八号”的轨道,由此可以判断()
| A.“天宫一号”的运行速率小于“神舟八号”的运行速率 |
| B.“天宫一号”和“神舟八号”的运行速率均大于第一宇宙速度 |
| C.“天宫一号”的周期小于“神舟八号”的周期 |
| D.“天宫一号”的向心加速度大于“神舟八号”的向心加速度 |
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的:
| A.运动周期相同 | B.运动线速度相同 |
| C.运动角速度相同 | D.向心加速度相同 |
如图所示,一根轻杆(质量不计)的一端 以O点为固定转轴,另一端固定一个小球,小球以O点为圆心在竖直平面内沿顺时针方向做匀速圆周运动。当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
| A.沿F1的方向 | B.沿F2的方向 |
| C.沿F3的方向 | D.沿F4的方向 |
如图所示的是杂技演员表演的“水流星”。一根细长绳的一端,系着一个盛了水的容器。以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动。N为圆周的最高点,M为圆周的最低点。若“水流星”通过最低点时的速度 。则下列判断正确的是( )
。则下列判断正确的是( )
| A.“水流星”到最高点时的速度为零 |
| B.“水流星”通过最高点时,有水从容器中流出 |
| C.“水流星”通过最高点时,水对容器底没有压力 |
| D.“水流星”通过最高点时,绳对容器有向下的拉力 |

