Question

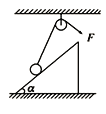
【题目】如图所示，用一块长L=1.0m的木板在墙和水平地面间架设斜面，斜面与水平地面的倾角θ可在0～60°间调节后固定．将质量m=0.2kg的小物块从斜面顶端静止释放，物块与斜面间的动摩擦因数μ1=0.05，物块与水平地面间的动摩擦因数μ2=0.8，忽略物块在斜面与水平地面交接处的能量损失．（已知重力加速度g=10m/s2；sin37°=0.6，cos37°=0.8最大静摩擦力等于滑动摩擦力）

（1）当θ角增大到多少时，物块恰能从斜面开始下滑；（用正切值表示）
（2）当θ角增大到37°时，物块沿斜面下滑时的加速度为多大？
（3）当θ角增大到多大时，物块停止时与墙面的距离最大，求此最大距离xm ．

Answer 1

【答案】
（1）解：物块恰能从斜面开始下滑时，有：

mgsinθ=μ1mgcosθ；

故得 tanθ=0.05；

答：当tanθ=0.05时，物块恰能从斜面开始下滑；

（2）解：当θ角增大到37°时，物块沿斜面匀加速下滑．

根据牛顿第二定律有 mgsinθ﹣μ1mgcosθ=ma

解得 a=5.6m/s2．

克服摩擦力做功Wf=μ1mgL1cosθ+μ2mg（L2﹣L1cosθ）

由动能定理得：mgL1sinθ﹣Wf=0

代入数据解得：

μ2=0.8；

答：当θ角增大到37°时，物块沿斜面下滑时的加速度为5.6m/s2．

（3）解：设物块停止时与墙面的距离为x．

对整个过程，由动能定理得：

mgLsinθ﹣μ1mgcosθL﹣μ2mg（x﹣Lcosθ）=0

代入数据整理得 x= （sinθ+0.75cosθ）= sin（θ+α）

其中 tanα=0.75，α=37°

根据数学知识知，当θ+α=90°，即θ=53°时x最大，最大值 xm= = m

答：当θ角增大到53°时，物块停止时与墙面的距离最大，此最大距离xm为 m．

【解析】（1）当物块刚好能从斜面开始下滑时，物体的重力沿斜面下滑的分力等于最大静摩擦力，列出等式即可求斜面的倾角θ；（2）当θ角增大到37°时，根据牛顿第二定律求物块下滑的加速度；（3）分段运用动能定理列式，得到物块停止时与墙面的距离x与θ的关系式，再由数学知识求得最大距离xm及此时斜面的倾角θ．
【考点精析】关于本题考查的动能定理的综合应用，需要了解应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷才能得出正确答案．