题目内容
【题目】(多选)如图所示,倾角θ=30°的光滑斜面体固定在水平面上,斜面长度L=0.8m,一质量m=1×10-3kg、带电量q=+1×10-4C的带电小球静止在斜面底端.现要使小球能够到达斜面顶端,可施加一沿斜面向上、场强大小为E=100V/m的匀强电场,重力加速度g=10 m/s2,则这个匀强电场存在的时间t可能为( )
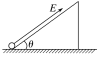
A.0.5s B.0.4s C.0.3s D.0.2s
【答案】AB
【解析】有电场时,根据牛顿定律可知:Eq-mgsin30°=ma1,解得a1=5m/s2,方向沿斜面向上;撤去电场时,小球的加速度a2=gsin 30°=5 m/s2,方向沿斜面向下;设电场存在的时间为t1,撤去电场后,恰好能到达斜面顶端,做减速运动的时间为t2,则a1t1=a2t2;且![]() a1t
a1t![]() +
+![]() a2t
a2t![]() =L;联立解得:t1=t2=0.4s,故要想使小球到达斜面顶端则电场存在的时间应该大于或等于0.4s.
=L;联立解得:t1=t2=0.4s,故要想使小球到达斜面顶端则电场存在的时间应该大于或等于0.4s.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目