题目内容
3.一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多),圆管中有两个直径与细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为v0.设A球运动到最低点时,B球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么m1,m2,R与v0应满足关系式是(m1-m2)$\frac{{v}_{0}^{2}}{R}$+(m1+5m2)g=0.分析 根据向心力的公式求出A球在最低点受到的向心力大小.A球运动到最低点时,B球恰好运动到最高点,若要此时两球作用于圆管的合力为零,即A、B两球对轨道的压力大小相等,方向相反.结合机械能守恒定律和牛顿第二定律求出m1、m2、R与v0应满足的关系式.
解答 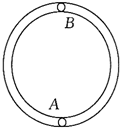 解:A球运动到最低点时速度为v0,A球受到向下重力mg和细管向上弹力N1的作用,其合力提供向心力.根据牛顿第二定律,得:
解:A球运动到最低点时速度为v0,A球受到向下重力mg和细管向上弹力N1的作用,其合力提供向心力.根据牛顿第二定律,得:
N1-m1g=m1$\frac{{v}_{0}^{2}}{R}$…①
这时B球位于最高点,设速度为v1,B球受向下重力m2g和细管弹力N2作用.球作用于细管的力是N1、N2的反作用力,要求两球作用于细管的合力为零,即要求N2与N1等值反向,N1=N2…②,
且N2方向一定向下,
对B球:N2+m2g=m2$\frac{{v}_{1}^{2}}{R}$…③
B球由最高点运动到最低点时速度为V0,此过程中机械能守恒定律,得:$\frac{1}{2}$m2v12+m2g•2R=$\frac{1}{2}$m2v02…④
由①②③④式消去N1、N2和V1后得到m1、m2、R与V0满足的关系式是:(m1-m2)$\frac{{v}_{0}^{2}}{R}$+(m1+5m2)g=0
故答案为:(m1-m2)$\frac{{v}_{0}^{2}}{R}$+(m1+5m2)g=0.
点评 本题是牛顿第二定律和机械能守恒定律的结合,关键要正确分析向心力的来源,明确在轨道的最高点和最低点,由合力提供向心力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.从地面竖直上抛物体A,同时在某高度有一物体B自由落下,两物体在空中相遇时的速率相等,则( )
| A. | 物体A的上抛初速度大小等于B落到地面时的速度大小 | |
| B. | 相遇时物体A已上升的高度和物体B已下落的高度相同 | |
| C. | 相遇时物体B的速度是物体A抛出速度的一半 | |
| D. | 物体A和物体B同时落地 |
11. 如图所示,质量分别为m1、m2、m3的三个物体用两根细线跨过定滑轮连在一起,静止时的位置如图所示,两根细线与水平面夹角分别为α和β,α<β,两根细线之间的夹角γ=90°,不计滑轮摩擦.若将质量为m2的物体质量减小一些,其余两个物体质量不变,则系统重新静止时,下列说法正确的是( )
如图所示,质量分别为m1、m2、m3的三个物体用两根细线跨过定滑轮连在一起,静止时的位置如图所示,两根细线与水平面夹角分别为α和β,α<β,两根细线之间的夹角γ=90°,不计滑轮摩擦.若将质量为m2的物体质量减小一些,其余两个物体质量不变,则系统重新静止时,下列说法正确的是( )
 如图所示,质量分别为m1、m2、m3的三个物体用两根细线跨过定滑轮连在一起,静止时的位置如图所示,两根细线与水平面夹角分别为α和β,α<β,两根细线之间的夹角γ=90°,不计滑轮摩擦.若将质量为m2的物体质量减小一些,其余两个物体质量不变,则系统重新静止时,下列说法正确的是( )
如图所示,质量分别为m1、m2、m3的三个物体用两根细线跨过定滑轮连在一起,静止时的位置如图所示,两根细线与水平面夹角分别为α和β,α<β,两根细线之间的夹角γ=90°,不计滑轮摩擦.若将质量为m2的物体质量减小一些,其余两个物体质量不变,则系统重新静止时,下列说法正确的是( )| A. | 两根细线对m3物体的拉力的合力将比原来减小 | |
| B. | 两根细线对m3物体的拉力的合力与原来相等 | |
| C. | 两根细线之间的夹角γ将比原来减小 | |
| D. | 两根细线之间的夹角γ与原来相等 |
18.如图所示,重力为G的物体放在倾角为θ的斜面上,静止不动.下面说法正确的是( )
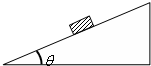

| A. | 物体一定受到静摩擦力作用,其方向沿斜面向下 | |
| B. | 物体受到重力,斜面的支持力,下滑力和静摩擦力作用 | |
| C. | 物体对斜面的压力就是重力在垂直于斜面方向上的分力 | |
| D. | 物体受到重力、斜面的支持力和静摩擦力的作用 |
8.关于物体的惯性,下列说法中错误的是( )
| A. | 骑自行车的人,上坡前要紧蹬几下,是为了增大惯性冲上坡 | |
| B. | 子弹从枪膛中射出后,在空中飞行速度逐渐减小,因此惯性也减小 | |
| C. | 宇航员在绕地球飞行的宇宙飞船中,可以“飘来飘去”,是因为他的惯性消失了 | |
| D. | 做自由落体运动的小球,速度越来越大,但惯性不变 |
15.下列说法中正确的是( )
| A. | 地球是质点 | |
| B. | 地球不是质点 | |
| C. | 在研究地球的公转时,可以把地球当作质点 | |
| D. | 在研究地面上的物体运动时,可以把地球当作质点 |
12. 为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:
为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:
(1)将金属块悬挂在该弹簧下方,静止时测得弹簧的伸长量为1.00cm,由此得出该弹簧在受到单位作用力时的伸长量,即F=kx式中的比例系数k为500N/m;
(2)将金属块放在长木板上,调节长木板的倾角,当金属块刚好能匀速下滑时测出斜面的高度为10.00cm,底边长为40.00cm,由此测得金属块和长木板间的动摩擦因数μ=0.25.
(3)如图1将木板固定在地面上,金属块放置于木板上.弹簧一端固定在竖直墙上,另一端与金属块接触,用手向左压金属块使弹簧压缩一定长度后由静止释放,滑块脱离弹簧后,又沿长木板滑行一段距离而停下.测出每次弹簧的压缩量x和金属块脱离弹簧后在长木板上滑行的距离s,将对应的数据填写在下面的表格中.
为验证结果是否符合猜想Ep=$\frac{1}{2}$kx2,则应该根据以上数据作出得图象为D;
A:μGs-x图象;B:μGs-x2图象;C:μG(s+x)-x图象;D:μG(s+x)-x2图象.
在图2的坐标系中作出你所选择的图象,请注明横纵坐标所代表的物理量及单位,并注明你所选的标度,由图可得到Ep和x2间的关系式为Ep=250x2则该同学的猜想是正确(填“正确”或者“错误”)的.
 为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:
为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:(1)将金属块悬挂在该弹簧下方,静止时测得弹簧的伸长量为1.00cm,由此得出该弹簧在受到单位作用力时的伸长量,即F=kx式中的比例系数k为500N/m;
(2)将金属块放在长木板上,调节长木板的倾角,当金属块刚好能匀速下滑时测出斜面的高度为10.00cm,底边长为40.00cm,由此测得金属块和长木板间的动摩擦因数μ=0.25.
(3)如图1将木板固定在地面上,金属块放置于木板上.弹簧一端固定在竖直墙上,另一端与金属块接触,用手向左压金属块使弹簧压缩一定长度后由静止释放,滑块脱离弹簧后,又沿长木板滑行一段距离而停下.测出每次弹簧的压缩量x和金属块脱离弹簧后在长木板上滑行的距离s,将对应的数据填写在下面的表格中.
| X/cm | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| S/cm | 3.00 | 6.02 | 10.05 | 14.96 | 20.97 | 28.05 |
A:μGs-x图象;B:μGs-x2图象;C:μG(s+x)-x图象;D:μG(s+x)-x2图象.
在图2的坐标系中作出你所选择的图象,请注明横纵坐标所代表的物理量及单位,并注明你所选的标度,由图可得到Ep和x2间的关系式为Ep=250x2则该同学的猜想是正确(填“正确”或者“错误”)的.
13.一个质点做变速直线运动的v-t图象如图,下列说法中正确的是( )
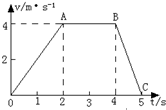

| A. | 第1s内与第5s内的速度方向相反 | |
| B. | 第1s内与第2s内的位移之比为1:4 | |
| C. | 第2s内与第5s内的加速度大小之比为1:2 | |
| D. | 质点在前2s内速度的变化量与第5s内速度的变化量相同 |
 某同学为了描绘一个“6V,9W”的电学器件的伏安特性曲线,并测出该电学器件在额定电压下的准确电阻值,到实验室寻找到了一些仪器,规格及数量如下:
某同学为了描绘一个“6V,9W”的电学器件的伏安特性曲线,并测出该电学器件在额定电压下的准确电阻值,到实验室寻找到了一些仪器,规格及数量如下: 表示)
表示)