题目内容
12. 为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:
为研究弹簧的弹性势能Ep和弹簧形变量x间的函数关系.某同学想设用水平力缓慢地将弹簧从原长拉伸x,该过程拉力做的功W等于弹性势能的增加,即Ep.根据本实验所得,弹力F和弹簧伸长x的关系为F=kx.拉力的平均值为$\frac{1}{2}$kx,所以W=$\frac{1}{2}$kx2.他猜想弹性势能的表达式应该就是Ep=$\frac{1}{2}$kx2.为了验证自己的猜想他找到一根弹簧、一个木板、一个重G=5.0N的长方体形金属块,设计了一个实验,利用一把毫米刻度尺来验证这个结论.步骤是:(1)将金属块悬挂在该弹簧下方,静止时测得弹簧的伸长量为1.00cm,由此得出该弹簧在受到单位作用力时的伸长量,即F=kx式中的比例系数k为500N/m;
(2)将金属块放在长木板上,调节长木板的倾角,当金属块刚好能匀速下滑时测出斜面的高度为10.00cm,底边长为40.00cm,由此测得金属块和长木板间的动摩擦因数μ=0.25.
(3)如图1将木板固定在地面上,金属块放置于木板上.弹簧一端固定在竖直墙上,另一端与金属块接触,用手向左压金属块使弹簧压缩一定长度后由静止释放,滑块脱离弹簧后,又沿长木板滑行一段距离而停下.测出每次弹簧的压缩量x和金属块脱离弹簧后在长木板上滑行的距离s,将对应的数据填写在下面的表格中.
| X/cm | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| S/cm | 3.00 | 6.02 | 10.05 | 14.96 | 20.97 | 28.05 |
A:μGs-x图象;B:μGs-x2图象;C:μG(s+x)-x图象;D:μG(s+x)-x2图象.
在图2的坐标系中作出你所选择的图象,请注明横纵坐标所代表的物理量及单位,并注明你所选的标度,由图可得到Ep和x2间的关系式为Ep=250x2则该同学的猜想是正确(填“正确”或者“错误”)的.
分析 (1)根据胡克定律F=k△x,即可求解;
(2)由受力分析,结合平衡条件,依据平行四边形定则与三角函数,即可求解;
(3)根据表格数据,结合动能定理,即可确定结果,并由图象的斜率,即可求解.
解答 解:(1)由胡克定律,则有:$k=\frac{F}{x}=\frac{G}{x}=500N/m$.
(2)金属块刚好能沿斜面匀速下滑,则有:mgsinθ=μmgcosθ,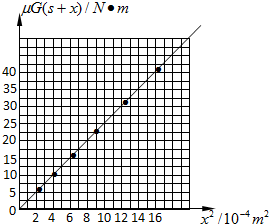 即得金属块和长木板间的动摩擦因数μ=tanθ=$\frac{h}{L}$=0.25.
即得金属块和长木板间的动摩擦因数μ=tanθ=$\frac{h}{L}$=0.25.
(3)由动能定理可知,EP=μG(S+x)
故要证明,Ep=$\frac{1}{2}$kx2应证明:
μG(S+x)=$\frac{1}{2}$kx2
故选:D;
根据图线求得Ep和x2间的关系式为Ep=250x2,
故EP=$\frac{1}{2}$kx2;
该同学的猜想是正确的
故答案为:(1)500;(2)0.25;(3)D,Ep=250x2,正确.
点评 本题借助于动能定理以及数学推导考查了弹性势能和弹性形变量之间的关系,是考查知识综合应用、公式理论推导的好题;要注意正确推导对应的方程式,从而得出正确的结论.

练习册系列答案
相关题目
2.关于弹力,下列说法不正确的是( )
| A. | 弹力的方向总是与施力物体形变的方向相反 | |
| B. | 轻绳中的弹力方向一定沿着绳并指向绳收缩的方向 | |
| C. | 轻杆中的弹力方向一定沿着轻杆 | |
| D. | 在弹性限度内;弹簧的弹力大小与弹簧的形变量成正比 |
20.松花江某支流恰呈东西走向,江水自西向东流动(江水中有大量电解质,可水解成正负离子).某处水面宽度L=200m,水流速度v=5m/s,在南北两岸靠岸水中放两正对的平行江岸的平板电极,用一毫伏表测量两极间电压U=40mv,则( )
| A. | 该处地磁场竖直分量BT=4.0×10-5T | B. | 该处地磁场竖直分量BT=2.0×10-5T | ||
| C. | 北岸电势高 | D. | 南岸电势高 |
7. 有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断.例如从解的物理量单位,解随某些已知量变化的趋势,解在一些特殊条件下的结果等方面进行分析,并与预期结果、实验结论等进行比较,从而判断解的合理性或正确性.举例如下:如图所示.质量为M、倾角为θ的滑块A放于水平地面上.把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+msi{n}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项( )
有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断.例如从解的物理量单位,解随某些已知量变化的趋势,解在一些特殊条件下的结果等方面进行分析,并与预期结果、实验结论等进行比较,从而判断解的合理性或正确性.举例如下:如图所示.质量为M、倾角为θ的滑块A放于水平地面上.把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+msi{n}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项( )
 有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断.例如从解的物理量单位,解随某些已知量变化的趋势,解在一些特殊条件下的结果等方面进行分析,并与预期结果、实验结论等进行比较,从而判断解的合理性或正确性.举例如下:如图所示.质量为M、倾角为θ的滑块A放于水平地面上.把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+msi{n}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项( )
有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断.例如从解的物理量单位,解随某些已知量变化的趋势,解在一些特殊条件下的结果等方面进行分析,并与预期结果、实验结论等进行比较,从而判断解的合理性或正确性.举例如下:如图所示.质量为M、倾角为θ的滑块A放于水平地面上.把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+msi{n}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项( )| A. | 当θ=0°时,该解给出a=0,这符合常识,说明该解可能是对的 | |
| B. | 当θ=90°时,该解给出a=g,这符合实验结论,说明该解可能是对的 | |
| C. | 当m>>M时,该解给出a=$\frac{g}{sinθ}$,这符合预期的结果,说明该解可能是对的 | |
| D. | 当M>>m时,该解给出a=gsinθ,这符合预期的结果,说明该解可能是对的 |
17.关于1eV,下列说法正确的是 ( )
| A. | 是1元电荷的电量1.60×10-19C | B. | 是1V的电势差 | ||
| C. | 是电场力做功1.60×10-19J | D. | 是电子产生的电场强度 |
4.大小分别是30N和25N的两个力,同时作用在一个物体上,对于合力F大小的估计最恰当的是( )
| A. | F=55 N | B. | 25N≤F≤30N | C. | 25N≤F≤55N | D. | 5N≤F≤55N |
1.对于质点的描述,下列说法中正确的是( )
| A. | 只要是小的物体就可看做质点 | |
| B. | 只要是做直线运动的物体就可看做质点 | |
| C. | 做曲线运动的物体都不能看做质点 | |
| D. | 在平直公路上行驶的汽车,当把汽车作为一个整体来研究它的运动时,可把汽车看做质点 |
 如图所示,是某质点运动的v-t图象,请回答:
如图所示,是某质点运动的v-t图象,请回答: