题目内容
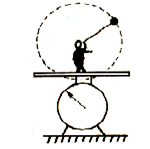
如图所示，一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨。槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T。有一个质量m=0.10g、带电量为q=+1.6×10-3C的小球在水平轨道上向右运动。若小球恰好能通过最高点，重力加速度g=10m/s2。求：
（1）小球在最高点所受的洛伦兹力F；
（2）小球的初速度v0。
（1）F=8×10-4N（2）v0=4.58m/s
解析试题分析：（1）设小球在最高点的速度为v，则由题意和左手定则得：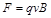
，方向竖直向上 ………………①
由于小球恰好能通过最高点，由牛顿第二定律有：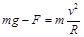
………………②
联解①②代入数据得：
F=8×10-4N ………………③
（2）由于轨道光滑，且洛伦兹力不做功，由机械能守恒定律可得：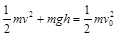
………………④
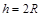………………⑤
联解④⑤代入数据得：
v0=4.58m/s ………………⑥
考点：考查了带电粒子在磁场中的运动，牛顿第二定律，机械能守恒定律
练习册系列答案
名校课堂系列答案
相关题目
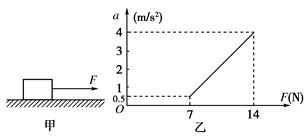
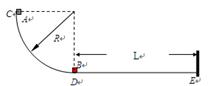
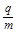＝1.0×108C/kg，初速度v0＝2×105m/s（粒子重力不计），在A、B两板间加上如图乙所示的电压，电压的周期T＝2.0×10－6s，t＝0时刻A板电势高于B板电势，两板间电场可视为匀强电场，电势差U0＝360V，A、B板右侧相距s＝2cm处有一边界MN，在边界右侧存在一垂直纸面向里的匀强磁场，磁感应强度B＝
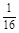T，磁场中放置一“＞”型荧光板，位置如图所示，板与水平方向夹角θ＝37°，不考虑粒子之间相互作用及粒子二次进入磁场的可能，求：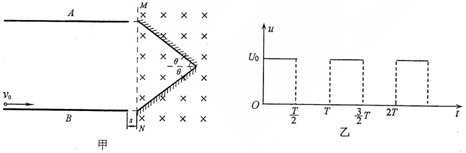
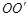为右边界的匀强磁场中，匀强磁场的磁感应强大小为B，方向垂直导轨平面向下，导轨右侧接有定值电阻R，导轨电阻忽略不计。在距边界
。
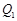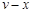图象如图乙所示。
。
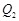