题目内容
如图，半径R=0.8m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点D与长为L的水平面相切于D点，质量M=1.0kg的小滑块A从圆弧顶点C由静止释放，到达最低点D点后，与D点m=0.5kg的静止小物块B相碰，碰后A的速度变为vA="2.0" m/s，仍向右运动．已知两物块与水平面间的动摩擦因数均为µ=0.1，A、B均可视为质点，B与E处的竖直挡板相碰时没有机械能损失，取g=10m/s2．求：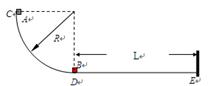
（1）滑块A刚到达圆弧的最低点D时对圆弧的压力；
（2）滑块B被碰后瞬间的速度；
（3）要使两滑块能发生第二次碰撞，DE的长度L应满足的条件．
（1）F＝30 N（2）vB＝4 m/s（3）L＜5m
解析试题分析：（1）设小滑块运动到D点的速度为v，由机械能守恒定律有：MgR＝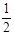
Mv2 (2分)
在D点，由牛顿第二定律有：F - Mg＝M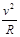
(2分)
联立得： F＝30 N (1分)
由牛顿第三定律，小滑块在D点时对圆弧的压力为30N (1分)
(2) 设B滑块被碰后的速度为vB，由动量守恒定律：M v＝MvA+mvB (3分)
得： vB＝4 m/s （1分）
(3) 由于B物块的速度较大，如果它们能再次相碰一定发生在B从竖直挡板弹回后，假设两物块能运动到最后停止，达到最大的路程，则
对于A物块，由动能定理：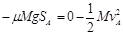
(2分)
解得：SA="2" m （1分）
对于B物块，由于B与竖直挡板的碰撞无机械能损失，由动能定理：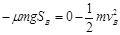
(2分)
解得：SB="8" m（1分）
两滑块刚好第二次发生接触的条件2L=SA+ SB="10" m （1分）
要使两滑块能发生第二次碰撞L＜5m （1分）
考点：考查了动能定理，动量守恒定律，牛顿运动定律
练习册系列答案
相关题目
、
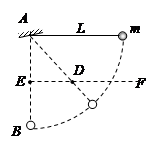
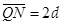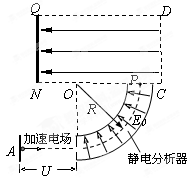
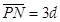，离子重力不计。