题目内容
（12分）如图所示，固定的光滑金属导轨间距为L，导轨电阻不计，上端a、b间接有阻值为R的电阻，导轨平面与水平面的夹角为θ，且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中，质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上．初始时刻，弹簧恰处于自然长度，导体棒具有沿轨道向上的初速度v0．整个运动过程中导体棒始终与导轨垂直并保持良好接触．已知弹簧的劲度系数为k，弹簧的中心轴线与导轨平行．
（1）求初始时刻通过电阻R的电流I的大小和方向；
（2）当导体棒第一次回到初始位置时，速度变为v，求此时导体棒的加速度大小a；
（3）导体棒最终静止时弹簧的弹性势能为Ep，求导体棒从开始运动直到停止的过程中，电阻R上产生的焦耳热Q．
（1）电流大小
，电流方向为b→a（2）
（3）
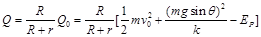
解析试题分析：（1）棒产生的感应电动势
通过
的电流大小，电流方向为b→a
（2）棒产生的感应电动势为
，感应电流
棒受到的安培力大小
，方向沿斜面向上
根据牛顿第二定律 有 
，解得
（3）导体棒最终静止，有 
，压缩量
设整个过程回路产生的焦耳热为Q0，根据能量守恒定律有
电阻R上产生的焦耳热
考点：考查了牛顿第二定律与电磁学综合，能量守恒定律，焦耳定律
练习册系列答案
相关题目
N
范围内选取），使粒子恰好从b板的T孔飞出，求粒子飞出时速度方向与b板板面夹角的所有可能值（可用反三角函数表示）。