题目内容
如图,一个质量为M的人,站在台秤上,手拿绳子一端,绳子另一端拴一个质量为m的小球,线长为R,让小球在竖直平面内作圆周运动,且摆球恰能通过圆轨道最高点,不计小球所受空气阻力。求小球作圆周运动过程中,台秤示数的变化范围。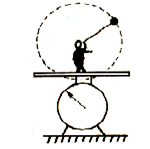
Mg?0.75mg (M+6m)g
解析试题分析:小球运动到最低点时悬线对人的拉力最大,且方向竖直向下,故台秤示数最大,小球通过最低点时,据牛顿第二定律有T?mg=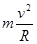 解得T=6mg
解得T=6mg
所以台秤的最大示数为F=(M+6m)g
当小球处于如图所示状态时,
设其速度为v1,由机械能守恒有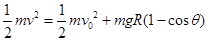
由牛顿第二定律有:T+mgcosθ=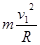
解得悬线拉力 T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=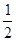 ,即θ=60°时,台秤的最小示数为Fmin=Mg?Ty=Mg?0.75mg.
,即θ=60°时,台秤的最小示数为Fmin=Mg?Ty=Mg?0.75mg.
考点:本题考查机械能守恒、牛顿运动定律、匀速圆周运动。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目


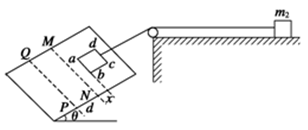
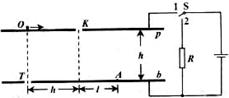
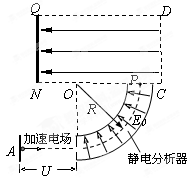
 范围内选取),使粒子恰好从b板的T孔飞出,求粒子飞出时速度方向与b板板面夹角的所有可能值(可用反三角函数表示)。
范围内选取),使粒子恰好从b板的T孔飞出,求粒子飞出时速度方向与b板板面夹角的所有可能值(可用反三角函数表示)。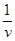 的关系如图所示.试求
的关系如图所示.试求
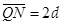 、
、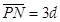 ,离子重力不计。
,离子重力不计。