题目内容
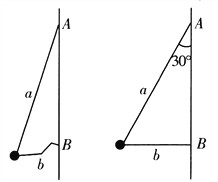
【题目】如图所示，一质量为m的小球用两根不可伸长的轻绳a、b连接，两轻绳的另一端分别系在竖直杆的A、B两点上，当两轻绳伸直时，a绳与杆的夹角为30°，b绳水平，已知a绳长为2L，当竖直杆以自己为轴转动，角速度
从零开始缓慢增大过程中，则下列说法正确的是( )
A. 从开始至b绳伸直但不提供拉力时，绳a对小球做功为0
B. b绳伸直但不提供拉力时，小球的向心加速度大小为
C. 从开始至b绳伸直但不提供拉力时，小球的机械能增加了
D. 当
时，b绳未伸直
【答案】BCD
【解析】当b绳刚要伸直时，对小球，由牛顿第二定律和向心力公式得水平方向有： 
，竖直方向有
，解得
，小球的机械能增加量为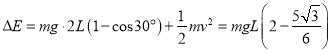
，由功能关系可知，从开始至b绳伸直但不提供拉力时，绳a对小球做功为
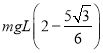，故A错误C正确；b绳刚好伸直无拉力时，小球的角速度为
，当
，所以b未伸直，小球的向心加速度为
，故BD正确．
练习册系列答案
备战中考寒假系列答案
相关题目
