题目内容
【题目】如图所示,小车上固定一水平横杆,横杆左端的固定斜杆与竖直方向成α角,斜杆下端连接一质量为m的小球;同时横杆右端用一根细线悬挂相同的小球.当小车沿水平面做直线运动时,细线与竖直方向间的夹角β(β≠α)保持不变.设斜杆、细线对小球的作用力分别为F1、F2 , 下列说法正确的是( )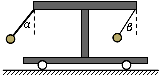
A.F1、F2大小不相等
B.F1、F2方向相同
C.小车加速度大小为gtanα
D.小车加速度大小为gtanβ
【答案】B,D
【解析】解:A、B、对右边的小铁球研究,根据牛顿第二定律,设其质量为m,得:
mgtanβ=ma,
得到:a=gtanβ
对左边的小铁球研究.设其加速度为a′,轻杆对小球的弹力方向与竖直方向夹角为θ,
由牛顿第二定律,得:
mgtanθ=ma′
因为a=a′,得到θ=β,则轻杆对小球的弹力方向与细线平行,即F1、F2方向相同,大小相等,A不符合题意,B符合题意;
C、D、小车的加速度a=gtanβ,C不符合题意,D符合题意.
故答案为:BD.
分别对两个小球进行受力分析,根据牛顿第二定律求出加速度,结合加速度之间的关系进行判断。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目





