题目内容
6. 如图所示,面积很大的水池,水深为H水面浮着一正方体木块,木块边长为a,密度为水的$\frac{1}{2}$,质量为m,开始时,木块静止,现用力F将木块缓慢往下压,求从开始到木块刚好完全没入水中的过程中,力F所做的功.
如图所示,面积很大的水池,水深为H水面浮着一正方体木块,木块边长为a,密度为水的$\frac{1}{2}$,质量为m,开始时,木块静止,现用力F将木块缓慢往下压,求从开始到木块刚好完全没入水中的过程中,力F所做的功.
分析 根据功能关系,力对木块做的功等于木块与水系统势能的增加量.由功能原理解答即可.
解答 解:因水池面积很大,可忽略因木块压入水中所引起的水深变化,在木块完全浸没过程中,木块的重力势能变化为:
△EP1=-mg•$\frac{a}{2}$
上式负号表示木块的重力势能减少,水的重力势能变化可理解为,木块一半体积的水上移至水面上,这部分水质量为m,上升高度为$\frac{3a}{4}$,故水的重力势能变化为:
△EP2=mg•$\frac{3a}{4}$
由功能关系知力F所做的功为:WF=△EP1+△Ep2=$\frac{mga}{4}$
答:从开始到木块刚好完全没入水的过程中,力F所作的功为$\frac{mga}{4}$.
点评 本题关键是分析清楚木块和水的运动情况,抓住木块下降重力做功和同体积的水上升重力做功即可,然后根据功能关系列式研究.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
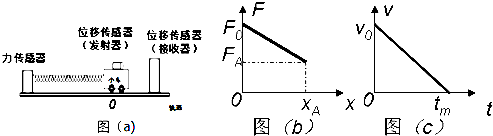
14.如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置(x)-时间(t)图线.由图可知( )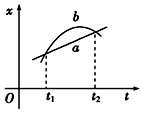

| A. | 在t1时刻,a、b两车相遇 | |
| B. | 在t2时刻,a、b两车运动方向相同 | |
| C. | 在t1到t2这段时间内,b车的速率先减小后增大 | |
| D. | 在t1到t2这段时间内,b车的速率一直比a车的大 |
1.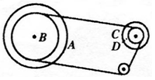 变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
 变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )| A. | 该自行车可变换两种不同挡位 | |
| B. | 该自行车可变换六种不同挡位 | |
| C. | 当A轮与D轮组合时,两轮的角速度之比ωA:ωD=1:4 | |
| D. | 当A轮与D轮组合时,两轮的角速度之比ωA:ωD=4:1 |