Question

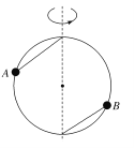
【题目】如图所示，质量均为m的带孔小球A、B穿在竖直面内的光滑金属网环上，金属圆环半径为R，用两根长均为R的细绳一端分别系于A、B球上，另一端分别系于金属圆环的最高点和最低点。现让金属圆环以角速度ω绕竖直直径转动，转动过程中细绳不会被拉断，则下列说法正确的是（　　）

A.当时，连接B球的细绳恰好被拉直

B.当时，金属圆环对A球的作用力为零

C.当，且ω不断增大时，金属圆环对B球的作用力有可能为零

D.当，且ω不断增大时，A球有可能会沿金属圆环向上移动

Answer 1

【答案】AB

【解析】

A．对B球研究，当连接B球的细绳恰好被拉直时

解得

故选项A正确；

B．连接B球的细绳恰好被拉直时，A球与B球具有相同的角速度，A球所受合力为

对A球受力分析可知，此时连接A球的细绳的拉力为2mg，所以A球不受金属圆环的作用力，故B正确；

C．当时，增大转动的角速度，连接B球的细绳上会有拉力，要维持B球竖直方向所受外力的合力为零，金属圆环对B球必定有弹力，故C错误；

D．当时，增大转动的角速度，金属圆环对A球的弹力不为零，由于竖直方向上A球和B球所受外力的合力均为零，可知细绳对A球的拉力应不断增大，因此A球不可能沿金属圆环向上移动，故D错误。

故选AB。