题目内容
3. 发射同步卫星需要有高超的技术,一般先用多级火箭,将卫星送入近地圆形轨道,此轨道称为初始轨道;当卫星飞临赤道上空时,控制火箭再次点火,短时间加速,卫星就会按椭圆轨道(也称转移轨道)运动;当卫星飞临远地点时,再次点火加速,卫星就最后进入同步轨道.如图所示为某次同步卫星发射的轨道示意图,椭圆轨道的近地点为A,远地点为B.假设A距地面高度为h,卫星在同步轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求:
发射同步卫星需要有高超的技术,一般先用多级火箭,将卫星送入近地圆形轨道,此轨道称为初始轨道;当卫星飞临赤道上空时,控制火箭再次点火,短时间加速,卫星就会按椭圆轨道(也称转移轨道)运动;当卫星飞临远地点时,再次点火加速,卫星就最后进入同步轨道.如图所示为某次同步卫星发射的轨道示意图,椭圆轨道的近地点为A,远地点为B.假设A距地面高度为h,卫星在同步轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求:(1)卫星在初始轨道上稳定运行时,经过A点的加速度aA的大小;
(2)卫星在同步轨道上稳定运行时的速度v的大小.
分析 (1)根据万有引力等于重力,以及牛顿第二定律求出经过A点的加速度大小.
(2)根据周期的大小,根据万有引力提供向心力,结合周期与线速度的关系求出卫星在同步轨道上稳定运行时的速度v的大小.
解答 解:(1)设地球的质量为M,卫星的质量为m,
卫星在A点:$G\frac{Mm}{(R+h)^{2}}=m{a}_{A}$,
对地面上质量为m0的物体:$G\frac{M{m}_{0}}{{R}^{2}}={m}_{0}g$,
解得${a}_{A}=\frac{{R}^{2}}{(R+h)^{2}}g$.
(2)卫星同步轨道上飞行的周期:T=$\frac{t}{n}$,
设同步轨道半径为r,则有:$\frac{GMm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$,
又v=$\frac{2πr}{T}$,
由以上各式解得v=$\root{3}{\frac{2πng{R}^{2}}{t}}$.
答:(1)经过A点的加速度aA的大小为$\frac{{R}^{2}}{(R+h)^{2}}g$;
(2)卫星在同步轨道上稳定运行时的速度v的大小为$\root{3}{\frac{2πng{R}^{2}}{t}}$.
点评 解决本题的关键掌握万有引力等于重力、万有引力提供向心力这两个重要理论,并能灵活运用.

练习册系列答案
相关题目
13. 某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )
某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )
 某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )
某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )| A. | 一定有光线从AC边射出 | |
| B. | 屏上、下两部分被照亮,中间存在未照亮的阴影,屏向左移动L刚好消除中间阴影 | |
| C. | 屏上、下两部分被照亮,中间存在未照亮的阴影,屏向右移动L刚好消除中间阴影 | |
| D. | 屏上被照亮部分的竖直总长度为4$\sqrt{3}$L |
14. 一矩形线圈,绕垂直于匀强磁场并位于线圈平面内的固定轴转动.线圈中的感生电动势e随时间t的变化如图所示.下面说法中正确的是( )
一矩形线圈,绕垂直于匀强磁场并位于线圈平面内的固定轴转动.线圈中的感生电动势e随时间t的变化如图所示.下面说法中正确的是( )
 一矩形线圈,绕垂直于匀强磁场并位于线圈平面内的固定轴转动.线圈中的感生电动势e随时间t的变化如图所示.下面说法中正确的是( )
一矩形线圈,绕垂直于匀强磁场并位于线圈平面内的固定轴转动.线圈中的感生电动势e随时间t的变化如图所示.下面说法中正确的是( )| A. | t1时刻通过线圈的磁通量为零 | |
| B. | t2时刻通过线圈的磁通量变化率的绝对值最大 | |
| C. | t3时刻通过线圈的磁通量变化率的绝对值最大 | |
| D. | 每当e变换方向时,通过线圈的磁通量绝对值都为最大 |
18.从同一地点先后开出n辆汽车组成车队在平直的公路上行驶,各车均由静止出发先做加速度为a的匀加速直线运动,达到同一速度v后改做匀速直线运动,欲使n辆车都匀速行驶时彼此距离均为s,则各辆车依次启动的时间间隔为(不计汽车的大小)( )
| A. | $\frac{2v}{a}$ | B. | $\frac{v}{2a}$ | C. | $\frac{s}{2v}$ | D. | $\frac{s}{v}$ |
8.如图所示,物体A和物体B与地面的动摩擦因素相等,在力F的作用下一起沿水平地面向右移动S,则( )


| A. | 摩擦力对A,B做功相等 | |
| B. | A、B动能的增量相同 | |
| C. | F对A做的功与A对B做的功相等 | |
| D. | 合力对A做的功与合外力对B做的功相等 |
13.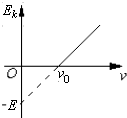 如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知不正确的是( )
如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知不正确的是( )
 如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知不正确的是( )
如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知不正确的是( )| A. | 该金属的逸出功等于E | |
| B. | 该金属的逸出功等于hν0 | |
| C. | 入射光的频率为2ν0时,产生的光电子的最大初动能为E | |
| D. | 入射光的频率为$\frac{{v}_{0}}{2}$时,产生的光电子的最大初动能为$\frac{E}{2}$ |
 如图所示,质量为M的重锤自h高度由静止开始下落,砸到质量为m的木楔上没有弹起,二者一起向下运动.设地层给它们的平均阻力为F.求:
如图所示,质量为M的重锤自h高度由静止开始下落,砸到质量为m的木楔上没有弹起,二者一起向下运动.设地层给它们的平均阻力为F.求:
 图中,设磁感应强度为0.001T,单匝线圈边长AB为20cm,宽AD为10cm,转速n为50r/s,求线圈转动时感应电动势的最大值.
图中,设磁感应强度为0.001T,单匝线圈边长AB为20cm,宽AD为10cm,转速n为50r/s,求线圈转动时感应电动势的最大值.