Question

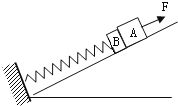
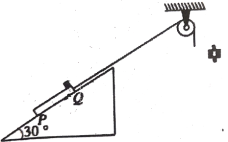
【题目】如图所示，固定斜面上放一木板PQ，木板的Q端放置一可视为质点的小物块，现用轻细线的一端连接木板的Q端，保持与斜面平行，绕过定滑轮后，另一端可悬挂钩码，钩码距离地面足够高.已知斜面倾角θ=30°，木板长为L，Q端距斜面顶端距离也为L，物块和木板的质量均为m，两者之间的动摩擦因数为μ1=.若所挂钩码质量为，物块和木板能一起匀速下滑。重力加速度为g，不计细线与滑轮之间的摩擦，设接触面间最大静摩擦力等于滑动摩擦力，.求

（1）木板与斜面间的动摩擦因数μ2;

（2）若不挂钩码，静止释放物块和木板后，物块和木板之间的摩擦力为多大?

（3）若所挂钩码的质量为3m时，静止释放物块和木板，求木板Q端到达斜面顶端所用时间。

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）绳中的拉力为，以物块和木板为对象，则

解得

（2）若不挂钩码，设静止释放物块和木板后两者一起沿斜面匀加速运动，故

对物块可得

联立解得

故假设正确，故

（3）若所挂钩码的质量为3m时，对钩码可得

设木板与物块发生相对滑动，则对木板可得

解得

物块的加速度为

故假设正确。物块滑到顶端时

解得