Question

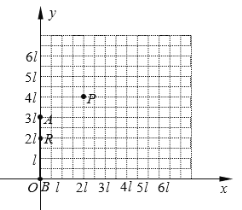
【题目】水平桌面上有两个玩具车A和B，两者用一轻质细橡皮筋相连，在橡皮筋上有一红色标记R。在初始时橡皮筋处于拉直状态，A、B和R分别位于直角坐标系中的（0，3l）、（0，0）和（0，2l）点。已知A从静止开始沿y轴正方向做匀加速直线运动，同时B沿x轴正方向以速度v做匀速直线运动。在两车此后运动的过程中，标记R在某时刻通过点P（2l，4l）。假定橡皮筋的伸长是均匀的，且在弹性限度内，求：

(1)标记R从静止开始运动到点P（2l，4l）的位移；

(2)A运动的加速度大小。

Answer 1

【答案】(1)，方向与x轴正方向成；(2)

【解析】

(1)标记R的位移

方向与x轴正方向成

即

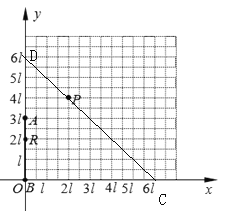
(2)因为开始时AR:BR=1：2，可知当R到达P点时DP:PC=1：2，根据相似三角形关系可知OC=BD=6l，则AD=3l，由运动公式

解得