题目内容
17.一小球被细绳拴着,在水平面内做半径为R的匀速圆周运动,向心加速度为a,那么说法中不正确的是( )| A. | 小球的角速度为ω=$\sqrt{\frac{a}{R}}$ | |
| B. | 小球在时间t内通过的路程s=t$\sqrt{aR}$ | |
| C. | 小球做匀速圆周运动的周期T=$\sqrt{\frac{a}{R}}$ | |
| D. | 小球在时间t内可能发生的最大位移为2R |
分析 根据圆周运动的向心加速度与角速度、线速度、周期的关系式即可求解.利用路程与线速度的关系求出路程.
解答 解:A、由向心加速度表达式a=Rω2,得:ω=$\sqrt{\frac{a}{R}}$,故A正确;
B、线速度大小为 v=Rω=$\sqrt{aR}$.路程等于速率乘以时间,故t时间内的路程为:s=vt=$\sqrt{aR}$t,故B正确.
C、周期可表示为:T=$\frac{2π}{ω}$=2π$\sqrt{\frac{R}{a}}$,故C错误.
D、圆周运动两点间的最大距离就是直径,故t时间内最大位移为2R,故D正确.
本题选择错误的,故选:C.
点评 描述圆周运动的物理量很多,关键在了解物理量的定义外,要熟悉各物理量之间的关系.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 布朗运动只能在液体里发生,且温度越高,布朗运动越激烈 | |
| B. | 分子间距离增大,分子间作用力可能为斥力 | |
| C. | 分子动能与分子势能的和叫做这个分子的内能 | |
| D. | 滴进水中的墨水微粒能做扩散运动,说明分子间有空隙 | |
| E. | 外界对某理想气体做功2.0×105J,气体对外放热1.0×105J,则气体温度升高 |
9.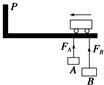 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )| A. | FA>FB>mg | B. | FA<FB<mg | C. | FA=FB=mg | D. | Fa=FB>mg |
6.下列说法正确的是( )
| A. | 太阳辐射的能量主要来自太阳内部的轻核聚变 | |
| B. | 轻核聚变与重核裂变均释放能量 | |
| C. | 根据玻尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| D. | 实验表明,只要照射光的强度足够大,就一定能发生光电效应现象 | |
| E. | 放射性元素衰变的快慢只由核内部自身的因素决定 |
7.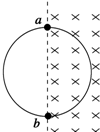 如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
 如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )| A. | 圆环具有扩张的趋势 | B. | 图中ab两点间的电压大小为$\frac{1}{4}$kπr2 | ||
| C. | 圆环中感应电流的大小为$\frac{krs}{2ρ}$ | D. | 圆环中产生顺时针方向的感应电流 |
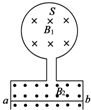 如图所示,圆形线圈和框架都处于竖直平面内,线圈面积S=2.0m2,B1是均匀变化的,质量m=4g、长度L=10cm的导体棒ab可在框架上无摩擦滑动,若B2=0.2T,闭合回路总电阻R=0.5Ω.当$\frac{△{B}_{1}}{t}$为何值时,导体棒可静止于线框上?B1应增强还是减弱?(g取10m/s2)
如图所示,圆形线圈和框架都处于竖直平面内,线圈面积S=2.0m2,B1是均匀变化的,质量m=4g、长度L=10cm的导体棒ab可在框架上无摩擦滑动,若B2=0.2T,闭合回路总电阻R=0.5Ω.当$\frac{△{B}_{1}}{t}$为何值时,导体棒可静止于线框上?B1应增强还是减弱?(g取10m/s2)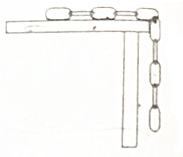 如图所示,一条质量为m,长为L的均匀铁链置于光滑水平桌面上,用手按住一端,使另一半下垂与桌边,放手后铁链下滑,当铁链全部脱离桌面的瞬间,重力对铁链做的功为$\frac{3mgL}{8}$;铁链的重力势能为-$\frac{mgL}{2}$(桌面高度h>L,取桌面为零势能参考平面).
如图所示,一条质量为m,长为L的均匀铁链置于光滑水平桌面上,用手按住一端,使另一半下垂与桌边,放手后铁链下滑,当铁链全部脱离桌面的瞬间,重力对铁链做的功为$\frac{3mgL}{8}$;铁链的重力势能为-$\frac{mgL}{2}$(桌面高度h>L,取桌面为零势能参考平面).