题目内容
18.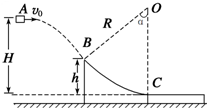 如图所示,从A点以v0的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,圆弧轨道BC的圆心角α=37°经圆孤轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,小物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,cos37°=0.8,sin37°=0.6,g=10m/s2.求:
如图所示,从A点以v0的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,圆弧轨道BC的圆心角α=37°经圆孤轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,小物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,cos37°=0.8,sin37°=0.6,g=10m/s2.求:(1)小物块水平抛出时,初速度v0的大小;
(2)小物块滑动至C点时,圆弧轨道对小球的支持力大小;
(3)试判断木板是否相对地面滑动,并求出木板至少为多长,才能保证小物块不滑出长木板?
分析 (1)已知平抛的抛出高度和落地速度方向,求落地的速度大小和方向,用运动的合成与分解求解;
(2)小物块在BC间做圆周运动运动,在C点时轨道支持力和重力的合力提供圆周运动的向心力,据此求解即可;
(3)根据物块在长木板上滑动时,物块的位移-长木板的位移应该小于等于长木板的长度这一临界条件展开讨论即可.
解答 解:(1)设小物块做平抛运动的时间为t,则有:H-h=$\frac{1}{2}$gt2
设小物块到达B点时竖直分速度为vy,有:vy=gt,
由以上两式代入数据解得:vy=3 m/s
由题意,速度方向与水平面的夹角为37°,有:tan 37°=$\frac{v_y}{v_0}$,
解得:v0=4 m/s
(2)设小物块到达C点时速度为v2,从B至C点,由动能定理得:
$mgh=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2$
设C点受到的支持力为FN,则有:
FN-mg=$\frac{mv_2^2}{R}$
由几何关系得:cosθ=$\frac{R-h}{R}$
由上式解得:R=0.75m,v2=2$\sqrt{7}$ m/s,FN=47.3 N
(3)由题意可知小物块对长木板的摩擦力为:Ff1=μ1mg=5 N
长木板与地面间的最大静摩擦力近似等于滑动摩擦力为:
Ff′2=μ2(M+m)g=10 N
因Ff1<Ff′2,所以小物块在长木板上滑动时,长木板静止不动
设小物块在长木板上做匀减速运动,至长木板最右端时速度刚好为0,则长木板长度为:l=$\frac{v_2^2}{{2{μ_1}g}}$=2.8 m
所以长木板至少为2.8 m,才能保证小物块不滑出长木板.
答:(1)小物块水平抛出时,初速度v0的大小4m/s;
(2)小物块滑动至C点时,对圆弧轨道C点的压力大小47.3 N;
(3)长木板至少为2.8 m,才能保证小物块不滑出长木板.
点评 本题关键要理清物块在多个不同运动过程中的运动规律,掌握物块各个阶段的运动规律是解决本题的关键.

| A. | 布朗运动只能在液体里发生,且温度越高,布朗运动越激烈 | |
| B. | 分子间距离增大,分子间作用力可能为斥力 | |
| C. | 分子动能与分子势能的和叫做这个分子的内能 | |
| D. | 滴进水中的墨水微粒能做扩散运动,说明分子间有空隙 | |
| E. | 外界对某理想气体做功2.0×105J,气体对外放热1.0×105J,则气体温度升高 |
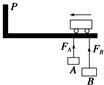 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )| A. | FA>FB>mg | B. | FA<FB<mg | C. | FA=FB=mg | D. | Fa=FB>mg |
| A. | 太阳辐射的能量主要来自太阳内部的轻核聚变 | |
| B. | 轻核聚变与重核裂变均释放能量 | |
| C. | 根据玻尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| D. | 实验表明,只要照射光的强度足够大,就一定能发生光电效应现象 | |
| E. | 放射性元素衰变的快慢只由核内部自身的因素决定 |
| A. | 速度不变的运动可能是曲线运动 | |
| B. | 速度变化的运动必定是曲线运动 | |
| C. | 加速度不变的运动可能是曲线运动 | |
| D. | 静止的物体在恒力作用下可能做曲线运动 |
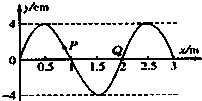 如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )
如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )| A. | 在t=0时刻,质点P和Q的速度方向均沿y轴正方向 | |
| B. | P点和Q点振动的周期均为0.4s | |
| C. | 在t=0到t=0.1s的时间里,Q点的速度在不断增大 | |
| D. | 在t=0.1s到t=0.2s的时间里,Q点的加速度在不断减小 |
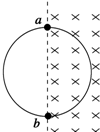 如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )| A. | 圆环具有扩张的趋势 | B. | 图中ab两点间的电压大小为$\frac{1}{4}$kπr2 | ||
| C. | 圆环中感应电流的大小为$\frac{krs}{2ρ}$ | D. | 圆环中产生顺时针方向的感应电流 |
 半径R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果球A经过N点时的速度v1=4m/s,A经过M点时对轨道的压力为0.5N.取g=10m/s2,求:
半径R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果球A经过N点时的速度v1=4m/s,A经过M点时对轨道的压力为0.5N.取g=10m/s2,求: