题目内容
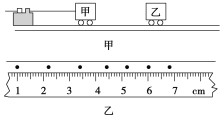
【题目】A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短).用闪光照相,闪光4次摄得的闪光照片如图所示.已知闪光的时间间隔为Δt,而闪光本身持续时间极短,在这4次闪光的瞬间,A、B两滑块均在0~80 cm刻度范围内,且第一次闪光时,滑块A恰好通过x=55 cm处,滑块B恰好通过x=70 cm处,问:
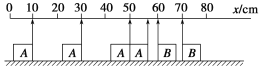
(1)碰撞发生在何处?
(2)碰撞发生在第一次闪光后多长时间?
(3)设两滑块的质量之比为mA∶mB=2∶3,试分析碰撞前后两滑块的质量与速度乘积之和是否相等?
【答案】(1)60 cm (2)![]() (3)碰撞前后两滑块的质量与速度乘积之和相等
(3)碰撞前后两滑块的质量与速度乘积之和相等
【解析】(1)据题意分析知:碰撞发生在第1、2两次闪光时刻之间,碰后B静止,故碰撞发生在x=60 cm处.
(2)碰撞后A向左做匀速运动,设其速度为vA′,则
vA′Δt=20
从发生碰撞后到第二次闪光时A向左运动10 cm,设时间为t′,则vA′t′=10
设第一次闪光到发生碰撞时间为t,则t+t′=Δt,
由以上各式得t=![]()
(3)取向右为正方向
碰撞前:A的速度vA=![]() ,B的速度为vB=-
,B的速度为vB=-![]() ,
,
质量与速度的乘积之和为mAvA+mBvB=mA×![]() +mB×
+mB×![]() =-mA×
=-mA×![]()
碰撞后:A的速度为vA′=-![]() ,B的速度为vB′=0,
,B的速度为vB′=0,
质量与速度的乘积之和为mAvA′+mBvB′=mA×![]() +0=-mA×
+0=-mA×![]()
由此可得碰撞前后两滑块的质量与速度乘积之和相等.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目