题目内容
8.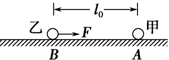 如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点间的距离为l0,释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=k$\frac{4Qq}{l_0^2}$(k为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.
如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点间的距离为l0,释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=k$\frac{4Qq}{l_0^2}$(k为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.(1)求乙球在释放瞬间的加速度大小;
(2)求乙球的速度最大时两个电荷间的距离.
分析 (1)乙球在释放瞬间竖直方向受力平衡,水平方向受到甲的静电斥力和F,根据牛顿第二定律求出其加速度大小.
(2)乙向左先做加速运动后做减速运动,当所受的甲的静电斥力和F大小相等时,乙球的速度最大,可求出两球间的距离.
解答 解:(1)根据牛顿第二定律得:ma=$\frac{kQq}{{{l}_{0}}^{2}}$-F,
又F=$\frac{kQq}{{{4l}_{0}}^{2}}$
可解得:a=$\frac{3kQq}{{{4l}_{0}}^{2}}$
(2)当乙球所受的甲的静电斥力和F大小相等时,乙球的速度最大,
F=$\frac{kQq}{{{4l}_{0}}^{2}}=\frac{kQq}{{x}^{2}}$
可解得:x=2l0
答:(1)求乙球在释放瞬间的加速度大小$\frac{3kQq}{{{4l}_{0}}^{2}}$;
(2)求乙球的速度最大时两个电荷间的距离2l0.
点评 本题是牛顿第二定律、动能定理的综合,根据乙球的受力情况,分析其运动情况是解题的基础.

练习册系列答案
相关题目
18.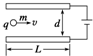 如图所示,一个质量为m、带电荷量为q的粒子,从两平行板左侧中点沿垂直场强方向射入,当入射速度为v时,恰好穿过电场而不碰金属板.要使粒子的入射速度变为$\frac{v}{2}$仍能恰好穿过电场,则必须再使( )
如图所示,一个质量为m、带电荷量为q的粒子,从两平行板左侧中点沿垂直场强方向射入,当入射速度为v时,恰好穿过电场而不碰金属板.要使粒子的入射速度变为$\frac{v}{2}$仍能恰好穿过电场,则必须再使( )
 如图所示,一个质量为m、带电荷量为q的粒子,从两平行板左侧中点沿垂直场强方向射入,当入射速度为v时,恰好穿过电场而不碰金属板.要使粒子的入射速度变为$\frac{v}{2}$仍能恰好穿过电场,则必须再使( )
如图所示,一个质量为m、带电荷量为q的粒子,从两平行板左侧中点沿垂直场强方向射入,当入射速度为v时,恰好穿过电场而不碰金属板.要使粒子的入射速度变为$\frac{v}{2}$仍能恰好穿过电场,则必须再使( )| A. | 粒子的电荷量变为原来的$\frac{1}{2}$ | B. | 两板间电压减为原来的$\frac{1}{2}$ | ||
| C. | 两板间距离变为原来的4倍 | D. | 两板间距离变为原来的2倍 |
16.火星成为我国深空探测的第二颗星球,假设火星探测器在着陆前,绕火星表面匀速飞行(不计周围其他天体的影响),航天员测出飞行N圈用时t,已知地球质量为M,地球半径为R,火星半径为r,地球表面重力加速度为g,则( )
| A. | 火星探测器匀速飞行的向心加速度约为$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$ | |
| B. | 火星探测器匀速飞行的速度约为$\frac{2πNR}{t}$ | |
| C. | 火星探测器的质量为$\frac{4π{N}^{2}{r}^{3}}{g{R}^{2}{t}^{2}}$ | |
| D. | 火星的平均密度为$\frac{3π{N}^{2}}{G{t}^{2}}$ |
3.在同一地点,甲、乙两物体沿同一方向做直线运动的速度-时间图象如图所示,则( ) 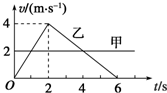

| A. | 两物体两次相遇的时刻是2 s末和6 s末 | |
| B. | 4 s后甲在乙后面 | |
| C. | 两物体相距最远的时刻是2 s末 | |
| D. | 乙物体先向前运动2 s,随后向后运动 |
13.下列关于质点说法正确的是( )
| A. | 质点就是指很小的物体 | |
| B. | 任何静止的物体都可以视为质点 | |
| C. | 在平直高速公路上行驶的汽车,可视为质点 | |
| D. | 体操运动员在做单臂大回环时,可视为质点 |
17.下列说法正确的是( )
| A. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| B. | “闻其声而不见其人”现象说明遇到同样障碍物时声波比可见光容易发生衍射 | |
| C. | 用超声波被血流反射回来其频率发生变化可测血流速度,这是利用多普勒效应 | |
| D. | 在双缝干涉实验中,用紫光代替黄光作为入射光可增大干涉条纹的间距 | |
| E. | 机械波和电磁波都可以在真空中传播 |
18.以下说法正确的是( )
| A. | 物体所带的电荷量是任意实数 | |
| B. | 物体所带电荷量的最小值是1.6×10-19 C | |
| C. | 元电荷就是电子或质子 | |
| D. | 凡试探电荷都是点电荷,凡点电荷都能作试探电荷 |
