题目内容
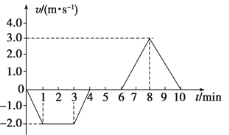
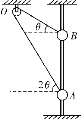
【题目】如图所示,Oa、Ob和ad是竖直平面内三根固定的光滑细杆,O、a、b、c、d位于同一圆周上,c为圆周的最高点,a为最低点,O′为圆心.每根杆上都套着一个小滑环,两个滑环从O点无初速释放,一个滑环从d点无初速释放,用t1、t2、t3分别表示滑环沿Oa、Ob、ad到达a、b所用的时间,则下列关系不正确的是 ( )
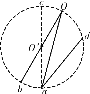
A. t2>t3B. t1=t2C. t1<t2D. t1=t3
【答案】B
【解析】
设ob与竖直方向的夹角为θ,由几何关系得oa与竖直方向的夹角为![]() ,
,
环沿oa下滑时的加速度大小为
![]()
沿ob下滑时的加速度大小为
a2=gcosθ
设ob长为L,由几何关系得oa长为![]() ,
,
根据运动学公式有
![]() ,
,![]()
得
![]() ,
,![]()
由此得到t1<t2;由于
![]()
同理可得到
![]()
因此
t1=t3,t2>t3
A.A项与上述计算结果相符,故A不符合题意;
B.B项与上述计算结果不相符,故B符合题意;
C.C项与上述计算结果相符,故C不符合题意;
D.D项与上述计算结果相符,故D不符合题意。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目