题目内容
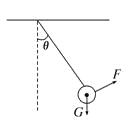
【题目】如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k，C为一固定挡板。系统处于静止状态。现开始用一恒力F沿斜面方向拉物块A使之向上运动，重力加速度g。求:
（1）物块B刚要离开C时物块A的加速度a
（2）从开始到此时物块A的位移d。
【答案】
【解析】
试题先对木块A受力分析，受重力，斜面的支持力和弹簧的弹力，根据共点力平衡条件求出弹簧的弹力后，再得到弹簧的压缩量；物块B刚要离开C时，先对物块B受力分析，受重力、支持力和弹簧的拉力，根据平衡条件求出弹簧弹力后进一步得到弹簧的伸长量，从而得到物体A的位移；最后再对物体A受力分析，受到拉力F、重力、支持力和弹簧的弹力，根据牛顿第二定律求出加速度．
解：令x1表示未加F时弹簧的压缩量，由胡克定律和共点力平衡条件可知
mAgsinθ=kx1①
令x2表示B刚要离开C时弹簧的伸长量，a表示此时A 的加速度，由胡克定律和牛顿定律可知
kx2=mBgsinθ ②
F﹣mAgsinθ﹣kx2=mAa ③
由②③式可得
a=
④
由题意
d=x1+x2⑤
由①②⑤式可得d=
即块B 刚要离开C时物块A的加速度为
，从开始到此时物块A的位移d为．
练习册系列答案
相关题目
