题目内容
13.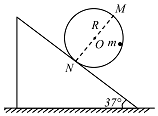 如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )| A. | 小球过M点时的速度等于$\sqrt{gR}$ | |
| B. | 小球过M点时的速度大于$\sqrt{gR}$ | |
| C. | 小球从M点运动到N点过程中重力势能变化量为2mgR | |
| D. | 小球从M点运动到N点过程中重力势能变化量为$\frac{8mgR}{5}$ |
分析 小球通过轨道最高点时恰好与轨道间没有相互作用力,故由重力提供向心力,根据圆周运动向心力公式即可得出最高点的速度;然后与M点的速度比较即可;根据重力做功求出小球重力势能的变化.
解答 解:A、设小球通过轨道最高点时速度的大小为v1,根据题意和圆周运动向心力公式得:
mg=m$\frac{{{v}_{1}}^{2}}{R}$
解得:v1=$\sqrt{gR}$
小球从M点到最高点的过程中,只有重力做负功,所以小球在最高点的速度小于小球在M点的速度.故A错误,B正确;
C、由几何关系可知,M与N之间的高度差:h=2Rcos37°=1.6R
所以小球从M点运动到N点过程中重力势能变化量为:△EP=WG=mgh=1.6mgR,故C错误,D正确.
故选:BD
点评 该题是动能定理及圆周运动向心力公式的直接应用,要抓住恰好到达最高点的隐含条件是由重力来提供向心力,难度不大,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
12. 如图所示为一质点作直线运动的速度-时间图象,下列说法中正确的是( )
如图所示为一质点作直线运动的速度-时间图象,下列说法中正确的是( )
 如图所示为一质点作直线运动的速度-时间图象,下列说法中正确的是( )
如图所示为一质点作直线运动的速度-时间图象,下列说法中正确的是( )| A. | 整个过程中,CD段和DE段的加速度大小相等,方向相反 | |
| B. | 整个过程中,BC段的加速度最大 | |
| C. | 整个过程中,D点所表示的状态,离出发点最远 | |
| D. | BC段所表示的运动通过的路程是34m |
13.根据机械波的知识可知( )
| A. | 横波沿水平方向传播,纵波沿竖直方向传播 | |
| B. | 在波的传播过程中,质点随波迁移将振动形式和能量传播出去 | |
| C. | 波的图象就是反映各质点在同一时刻不同位移的曲线 | |
| D. | 机械波中各质点振动的频率与波源的振动频率相同 |
1.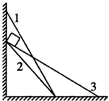 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
 将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )
将三个木板1、2、3固定在墙角,木板与墙壁和地面构成了三个不同的三角形,如图所示,其中1与2底边相同,2和3高度相同.现将一个可视为质点的物块分别从三个木板的顶端由静止释放,并沿木板下滑到底端,物块与木板之间的动摩擦因数μ均相同.在这三个过程中,下列说法正确的是( )| A. | 沿着木板1和木板2下滑到底端时,物块速度的大小相等 | |
| B. | 沿着木板2和木板3下滑到底端时,物块速度的大小相等 | |
| C. | 沿着木板1下滑到底端时,物块的动能最大 | |
| D. | 物块沿着木板3下滑到底端的过程中,产生的热量最多 |
8.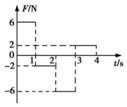 质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )
质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )
 质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )
质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )| A. | 2s末物体离出发点最远 | |
| B. | 4s末物体离出发点最远 | |
| C. | 前2s内和后2s内物体所受摩擦力相同 | |
| D. | 4s内物体的平均速率为2m/s |
3.火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( )
| A. | 太阳位于木星运行轨道的中心 | |
| B. | 火星和木星绕太阳运行速度的大小始终相等 | |
| C. | 火星与木星公转周期的平方之比等于它们轨道半长轴的立方之比 | |
| D. | 相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积 |
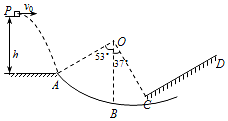 如图,半径R=1.0m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接,O为圆弧轨道ABC的圆心,B点为圆弧轨道的最低点,半径OA、OC与OB的夹角分别为53°和37°,将一个质量m=1.0kg的物体(视为质点)从A点左侧高为h=0.8m处的P点水平抛出,恰从A点沿切线方向进入圆弧轨道,已知物体与轨道CD间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图,半径R=1.0m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接,O为圆弧轨道ABC的圆心,B点为圆弧轨道的最低点,半径OA、OC与OB的夹角分别为53°和37°,将一个质量m=1.0kg的物体(视为质点)从A点左侧高为h=0.8m处的P点水平抛出,恰从A点沿切线方向进入圆弧轨道,已知物体与轨道CD间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求: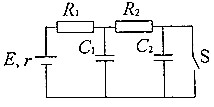 如图所示的电路,电源电动势E=6v,内阻r=1Ω,R1=2Ω,R3=3Ω,C1=C2=10μF,先把S接通,达到稳定后断开S,此后,流过R1的电流方向为向右(填“向左”或“向右”),流过R1的电量为2.7×10-4C.
如图所示的电路,电源电动势E=6v,内阻r=1Ω,R1=2Ω,R3=3Ω,C1=C2=10μF,先把S接通,达到稳定后断开S,此后,流过R1的电流方向为向右(填“向左”或“向右”),流过R1的电量为2.7×10-4C.