题目内容
2.如图(甲)所示,木杆OA可绕轴O在竖直平面内转动,某同学用此装置探究穿杆小球在力F作用下加速度与斜面倾角的关系.已知小球的质量m=1kg,小球与木杆之间的动摩擦因数μ=0.2,拉力F=8N,方向始终平行杆向上,假定小球与木杆间的最大静摩擦力始终等于滑动摩擦力,g=10m/s2.试求: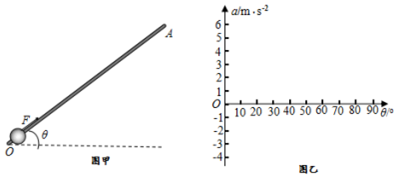
(1)当θ=0°时,小球的加速度大小a0;
(2)若木杆长L=1.9m,倾角为37°,小球在F的作用下由O点开始运动,为保证物块不冲出顶端A,力F最多作用多长时间;(取sin37°=0.6,cos37°=0.8)
(3)若力F始终作用在小球上,试通过计算推理,在图(乙)所示坐标系中,作出θ由0o增大到90o过程中α随θ变化关系图线.(sin40.4°=$\frac{20-\sqrt{10}}{26}$,sin63°=$\frac{20+\sqrt{10}}{26}$)
分析 (1)纵坐标交点表示木板水平放置时的加速度,根据牛顿第二定律即可求解;
(2)根据牛顿第二定律分别求出有F和撤去F时的加速度,根据匀变速直线运动的基本公式求出这两个过程的位移,根据两段位移之和为L求解.
(3)根据牛顿第二定律写出加速度随θ变化的函数表达式,画出对应的图象
解答 解:(1)当木板水平放置时,物块的加速度为a0,
滑动摩擦力f=μN=μmg=0.2×1×10=2(N)
${a}_{0}^{\;}=\frac{F-f}{m}=\frac{8-2}{1}m/{s}_{\;}^{2}=6m/{s}_{\;}^{2}$
(2)力F作用时的加速度大小:
${a}_{1}^{\;}=\frac{F-mgsin37°-μmgcos37°}{m}$=$\frac{8-10×0.6-0.2×10×0.8}{1}=0.4m/{s}_{\;}^{2}$
撤去力F后的加速度大小:${a}_{2}^{\;}=\frac{mgsin37°+μmgcos37°}{m}$=$\frac{10×0.6+0.2×10×0.8}{1}=7.6m/{s}_{\;}^{2}$
由题意有 $L={s}_{1}^{\;}+{s}_{2}^{\;}$
即 $1.9=\frac{1}{2}×0.4×{t}_{\;}^{2}+\frac{(0.4t)_{\;}^{2}}{2×7.6}$
解得:t≈3.0s
(3)对小球:F-mgsinθ-μmgcosθ=ma
得:a=8-10sinθ-2cosθ
当a=0时:8-10sinθ-2cosθ=0
得:$sinθ=\frac{20±\sqrt{10}}{26}$
即:40.4°≤θ≤63°时,a=0
在:0°≤θ<40.4°内:$a=8-\sqrt{104}sin(θ+φ)$(tanφ=0.2)
当θ=0°时:${a}_{1}^{\;}=6m/{s}_{\;}^{2}$
在63°<θ≤90°内:F-mgsinθ+μmgcosθ=ma
得:a=8-10sinθ+2cosθ
$a=8-\sqrt{104}sin(θ-φ)$(tanφ=0.2)
当θ=90°时:${a}_{2}^{\;}=-2m/{s}_{\;}^{2}$
所以:a随θ变化关系图线如图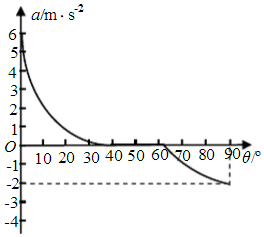
答:(1)当θ=0°时,小球的加速度大小${a}_{0}^{\;}$为$6m/{s}_{\;}^{2}$;
(2)若木杆长L=1.9m,倾角为37°,小球在F的作用下由O点开始运动,为保证物块不冲出顶端A,力F最多作用3.0s时间;
(3)若力F始终作用在小球上,试通过计算推理,在图(乙)所示坐标系中,作出θ由0o增大到90o过程中α随θ变化关系图线,如上图所示
点评 本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们能根据图象得出有效信息,难度适中.

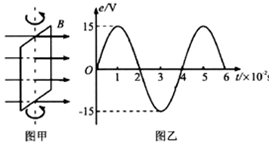 如图甲所示,在匀强磁场中,一矩形金属线圈绕与磁感线垂直的轴匀速转动,产生的电动势图象如图乙所示,则( )
如图甲所示,在匀强磁场中,一矩形金属线圈绕与磁感线垂直的轴匀速转动,产生的电动势图象如图乙所示,则( )| A. | t=0时刻穿过线圈平面的磁通量为零 | |
| B. | 线圈的转速为50r/s | |
| C. | 电动势有效值为15V | |
| D. | 电动势的变化频率为25Hz |
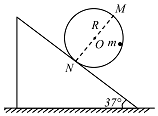 如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )| A. | 小球过M点时的速度等于$\sqrt{gR}$ | |
| B. | 小球过M点时的速度大于$\sqrt{gR}$ | |
| C. | 小球从M点运动到N点过程中重力势能变化量为2mgR | |
| D. | 小球从M点运动到N点过程中重力势能变化量为$\frac{8mgR}{5}$ |
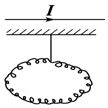 如图所示,一个有弹性的金属圆环被一根橡皮绳吊于通电直导线的正下方,直导线与圆环在同一竖直面内,当通电直导线中电流增大时,弹性圆环的面积S和橡皮绳的长度l将( )
如图所示,一个有弹性的金属圆环被一根橡皮绳吊于通电直导线的正下方,直导线与圆环在同一竖直面内,当通电直导线中电流增大时,弹性圆环的面积S和橡皮绳的长度l将( )| A. | S增大,l变长 | B. | S减小,l变短 | C. | S减小,l变长 | D. | S增大,l变短 |
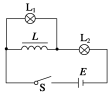 如图所示,线圈L的自感系数很大,且其直流电阻可以忽略不计,L1、L2是两个完全相同的小灯泡,开关S闭合和断开的过程中,灯L1、L2的亮度变化情况是(灯丝不会断)( )
如图所示,线圈L的自感系数很大,且其直流电阻可以忽略不计,L1、L2是两个完全相同的小灯泡,开关S闭合和断开的过程中,灯L1、L2的亮度变化情况是(灯丝不会断)( )| A. | S闭合,L1亮度不变,L2亮度逐渐变亮,最后两灯一样亮;S断开,L2立即熄灭,L1逐渐变暗 | |
| B. | S闭合,L1亮度不变,L2很亮;S断开,L1、L2立即熄灭 | |
| C. | S闭合,L1、L2同时亮,而后L1逐渐熄灭,L2亮度不变;S断开,L2立即熄灭,L1亮一下再熄灭 | |
| D. | S闭合,L1、L2同时亮,而后L1逐渐熄灭,L2则逐渐变得更亮;S断开,L2立即熄灭,L1亮一下再熄灭 |
| A. | kg、J、N是导出单位 | |
| B. | 在国际单位制中,牛顿第二定律的表达式是F=ma | |
| C. | kg、m、s是基本单位 | |
| D. | 单位制中的导出单位可以用基本单位来表达 |
| A. | 只要物体质量很小,就可以看成质点 | |
| B. | 只要物体体积很小,就可以看成质点 | |
| C. | 只要物体是球体,就可以看成质点 | |
| D. | 质点既具有数学特征,又具有物理属性 |
 如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )
如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )| A. | 甲比乙先出发 | B. | 甲和乙从同一地方出发 | ||
| C. | 甲的运动速率大于乙的运动速率 | D. | 甲的出发点在乙前面S0处 |
| A. | 凡轻小的物体皆可看作质点,而体积较大的物体不能看作质点 | |
| B. | 作息时间表上的数字表示时间间隔 | |
| C. | 物体做单向直线运动时,其位移就是路程 | |
| D. | 跳水运动员起跳后,到达最高点的速度为瞬时速度 |