题目内容
18.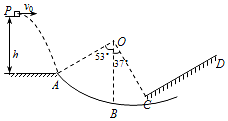 如图,半径R=1.0m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接,O为圆弧轨道ABC的圆心,B点为圆弧轨道的最低点,半径OA、OC与OB的夹角分别为53°和37°,将一个质量m=1.0kg的物体(视为质点)从A点左侧高为h=0.8m处的P点水平抛出,恰从A点沿切线方向进入圆弧轨道,已知物体与轨道CD间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图,半径R=1.0m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接,O为圆弧轨道ABC的圆心,B点为圆弧轨道的最低点,半径OA、OC与OB的夹角分别为53°和37°,将一个质量m=1.0kg的物体(视为质点)从A点左侧高为h=0.8m处的P点水平抛出,恰从A点沿切线方向进入圆弧轨道,已知物体与轨道CD间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:(1)物体水平抛出时的初速度大小v0;
(2)物体经过B点时受圆弧轨道支持力大小FN;
(3)物体在轨道CD上向上运动的最大距离x.
分析 (1)物体做平抛运动,由自由落体运动的规律求出物体落在A时的竖直分速度,然后应用运动的合成与分解求出物体的初速度大小v0.
(2)通过计算分析清楚物体的运动过程,由能量守恒定律求出物体在B点的速度,然后又牛顿第二定律求出物体对圆弧轨道压力大小FN;
(3)先由机械能守恒求出物体在C点的速度,然后由动能定理即可求解.
解答 解:(1)物体在抛出后竖直方向做自由落体运动,竖直方向:${v}_{y}=\sqrt{2gh}=\sqrt{2×10×0.8}m/s=4$m/s
物体恰从A点沿切线方向进入圆弧轨道,则:$\frac{{v}_{y}}{{v}_{0}}=tan53°$
得:${v}_{0}=\frac{{v}_{y}}{tan53°}=\frac{4}{\frac{4}{3}}m/s=3$m/s
(2)物体到达A点的速度:$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{{4}^{2}+{3}^{2}}m/s=5$m/s
A到B的过程中机械能守恒,得:$\frac{1}{2}m{v}^{2}+mgR(1-cos53°)=\frac{1}{2}m{v}_{B}^{2}$
物体在B点受到的支持力与重力的合力提供向心力,则:${F}_{N}-mg=\frac{m{v}_{B}^{2}}{R}$
得:FN=43N;
(3)B到C的过程中机械能守恒,得:$\frac{1}{2}m{v}_{C}^{2}+mgR(1-cos37°)=\frac{1}{2}m{v}_{B}^{2}$
得:${v}_{C}=\sqrt{27}$m/s
物体在斜面CD上受到的摩擦力:f=μmgcos37°=0.5×1.0×10×0.8N=4N
设物体在轨道CD上运动的距离x,则:$-fx-mg•xsin37°=0-\frac{1}{2}m{v}_{C}^{2}$
解得:x=1.45m;
答:(1)物体水平抛出时的初速度大小是3m/s;
(2)物体经过B点时受圆弧轨道支持力大小是43N;
(3)物体在轨道CD上向上运动的最大距离是1.45m.
点评 该题过程比较多,解答本题关键是分析清楚物体的运动情况,然后根据动能定理、平抛运动知识、能量守恒定理解题.

 阅读快车系列答案
阅读快车系列答案
| A. | 2.0×10-3T 方向水平向右 | B. | 5.0×10-3T 方向水平向右 | ||
| C. | 2.0×10-3T 方向水平向左 | D. | 5.0×10-3T 方向水平向左 |
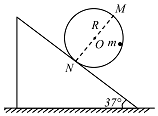 如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )| A. | 小球过M点时的速度等于$\sqrt{gR}$ | |
| B. | 小球过M点时的速度大于$\sqrt{gR}$ | |
| C. | 小球从M点运动到N点过程中重力势能变化量为2mgR | |
| D. | 小球从M点运动到N点过程中重力势能变化量为$\frac{8mgR}{5}$ |
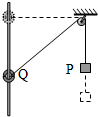 轻绳一端通过光滑的定滑轮与物块P连接,另一端与套在光滑竖直杆上的圆环Q连接,Q从静止释放后,上升一定距离到达与定滑轮等高处,则在此过程中( )
轻绳一端通过光滑的定滑轮与物块P连接,另一端与套在光滑竖直杆上的圆环Q连接,Q从静止释放后,上升一定距离到达与定滑轮等高处,则在此过程中( )| A. | 任意时刻P、Q两物体的速度大小满足vP<vQ | |
| B. | 任意时刻Q受到的拉力大小与P的重力大小相等 | |
| C. | 物块P的机械能守恒 | |
| D. | 当Q上升到与P等高时,它的机械能最大 |
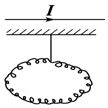 如图所示,一个有弹性的金属圆环被一根橡皮绳吊于通电直导线的正下方,直导线与圆环在同一竖直面内,当通电直导线中电流增大时,弹性圆环的面积S和橡皮绳的长度l将( )
如图所示,一个有弹性的金属圆环被一根橡皮绳吊于通电直导线的正下方,直导线与圆环在同一竖直面内,当通电直导线中电流增大时,弹性圆环的面积S和橡皮绳的长度l将( )| A. | S增大,l变长 | B. | S减小,l变短 | C. | S减小,l变长 | D. | S增大,l变短 |
| A. | kg、J、N是导出单位 | |
| B. | 在国际单位制中,牛顿第二定律的表达式是F=ma | |
| C. | kg、m、s是基本单位 | |
| D. | 单位制中的导出单位可以用基本单位来表达 |


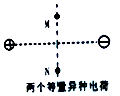

 如图所示,质量为m的物体被两根细绳OA、OB挂在小车上,两根细绳与车顶水平面夹角分别为53°和37°.试求:已知(cos37°=0.8,sin37°=0.6,cot37°=$\frac{4}{3}$).
如图所示,质量为m的物体被两根细绳OA、OB挂在小车上,两根细绳与车顶水平面夹角分别为53°和37°.试求:已知(cos37°=0.8,sin37°=0.6,cot37°=$\frac{4}{3}$). 如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )
如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )