题目内容
3.火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( )| A. | 太阳位于木星运行轨道的中心 | |
| B. | 火星和木星绕太阳运行速度的大小始终相等 | |
| C. | 火星与木星公转周期的平方之比等于它们轨道半长轴的立方之比 | |
| D. | 相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积 |
分析 熟记理解开普勒的行星运动三定律:
第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等.
第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
解答 解:A、根据开普勒第一定律的内容为:所有行星分别沿不同大小的椭圆轨道绕太阳运动,太阳处于椭圆的一个焦点上,故A错误;
B、第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等.行星在此椭圆轨道上运动的速度大小不断变化,故B错误;
C、根据开普勒第三定律,$\frac{{R}^{3}}{{T}^{2}}$=K,K为常数,火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方.故C正确;
D、根据开普勒第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等,是对同一个行星而言,故D错误;
故选:C
点评 正确理解开普勒的行星运动三定律是解答本题的关键.注意第三定律,$\frac{{R}^{3}}{{T}^{2}}$=K中,R是半长轴,T是公转周期,K与中心体有关.

练习册系列答案
相关题目
13.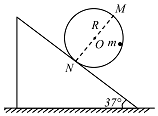 如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
 如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )
如图所示,一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上,圆轨道与斜面相切于N点,MN为圆轨道的直径.一个质量为m的小球恰好能在圆轨道内侧做圆周运动.重力加速度为g,sin37°=0.6,cos37°=0.8.则( )| A. | 小球过M点时的速度等于$\sqrt{gR}$ | |
| B. | 小球过M点时的速度大于$\sqrt{gR}$ | |
| C. | 小球从M点运动到N点过程中重力势能变化量为2mgR | |
| D. | 小球从M点运动到N点过程中重力势能变化量为$\frac{8mgR}{5}$ |
14.关于质点概念,下列说法中正确的是( )
| A. | 只要物体质量很小,就可以看成质点 | |
| B. | 只要物体体积很小,就可以看成质点 | |
| C. | 只要物体是球体,就可以看成质点 | |
| D. | 质点既具有数学特征,又具有物理属性 |
11. 如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )
如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )
 如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )
如图是在同一直线上运动的物体甲、乙的位移图象.由图象可知是( )| A. | 甲比乙先出发 | B. | 甲和乙从同一地方出发 | ||
| C. | 甲的运动速率大于乙的运动速率 | D. | 甲的出发点在乙前面S0处 |
18. 如图所示,在竖直平面有一个光滑的圆弧轨道MN,其下端(即N端)与表面粗糙的水平传送带左端相切,轨道N端与传送带左端的距离可忽略不计.当传送带不动时,将一质量为m的小物块(可视为质点)从光滑轨道上的P位置由静止释放,小物块以速度v1滑上传送带,从它到达传送带左端开始计时,经过时间t1,小物块落到水平地面的Q点;若传送带以恒定速率v2沿顺时针方向运行,仍将小物块从光滑轨道上的P位置由静止释放,同样从小物块到达传送带左端开始计时,经过时间t2,小物块落至水平地面.关于此时物块的运动,下列说法中正确的是( )
如图所示,在竖直平面有一个光滑的圆弧轨道MN,其下端(即N端)与表面粗糙的水平传送带左端相切,轨道N端与传送带左端的距离可忽略不计.当传送带不动时,将一质量为m的小物块(可视为质点)从光滑轨道上的P位置由静止释放,小物块以速度v1滑上传送带,从它到达传送带左端开始计时,经过时间t1,小物块落到水平地面的Q点;若传送带以恒定速率v2沿顺时针方向运行,仍将小物块从光滑轨道上的P位置由静止释放,同样从小物块到达传送带左端开始计时,经过时间t2,小物块落至水平地面.关于此时物块的运动,下列说法中正确的是( )
 如图所示,在竖直平面有一个光滑的圆弧轨道MN,其下端(即N端)与表面粗糙的水平传送带左端相切,轨道N端与传送带左端的距离可忽略不计.当传送带不动时,将一质量为m的小物块(可视为质点)从光滑轨道上的P位置由静止释放,小物块以速度v1滑上传送带,从它到达传送带左端开始计时,经过时间t1,小物块落到水平地面的Q点;若传送带以恒定速率v2沿顺时针方向运行,仍将小物块从光滑轨道上的P位置由静止释放,同样从小物块到达传送带左端开始计时,经过时间t2,小物块落至水平地面.关于此时物块的运动,下列说法中正确的是( )
如图所示,在竖直平面有一个光滑的圆弧轨道MN,其下端(即N端)与表面粗糙的水平传送带左端相切,轨道N端与传送带左端的距离可忽略不计.当传送带不动时,将一质量为m的小物块(可视为质点)从光滑轨道上的P位置由静止释放,小物块以速度v1滑上传送带,从它到达传送带左端开始计时,经过时间t1,小物块落到水平地面的Q点;若传送带以恒定速率v2沿顺时针方向运行,仍将小物块从光滑轨道上的P位置由静止释放,同样从小物块到达传送带左端开始计时,经过时间t2,小物块落至水平地面.关于此时物块的运动,下列说法中正确的是( )| A. | 小物块的落地点可能仍在Q点 | B. | 小物块的落地点可能在Q点右侧 | ||
| C. | 若v2<v1,仍可能有t2=t1 | D. | 若v2<v1,不可能有t2<t1 |
15.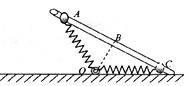 如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )
如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )
 如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )
如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )| A. | 小球可以返回到出发点A处 | |
| B. | 弹簧具有的最大弹性势能为$\frac{1}{2}$mv2 | |
| C. | 撤去弹簧,小球可以在直杆上处于静止 | |
| D. | aA-aC=g |
12.下列说法中正确的是( )
| A. | 凡轻小的物体皆可看作质点,而体积较大的物体不能看作质点 | |
| B. | 作息时间表上的数字表示时间间隔 | |
| C. | 物体做单向直线运动时,其位移就是路程 | |
| D. | 跳水运动员起跳后,到达最高点的速度为瞬时速度 |
1.一台电动机,额定电压是100V,电阻是1Ω,正常工作时,通过的电流为5A,则电动机的转动功率为( )
| A. | 500W | B. | 25W | C. | 2000W | D. | 475W |
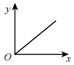
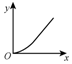
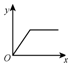
 如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )
如图,在一端封闭、长约E的玻璃管内注满清水,水中放一个红蜡做的小圆柱体R.将玻璃管的开口端用橡胶塞塞紧.若仅将玻璃管倒置,蜡块R将沿玻璃管向上匀加速一小段距离后开始匀速上升.若将玻璃管倒置的同时,将玻璃管沿水平方向向右匀速移动.设竖直向上为y轴,水平向右为x轴,则红蜡块R的运动轨迹可能是以下四个图中( )