题目内容
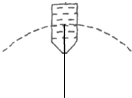
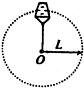
杂技演员表演“水流星”在长为L=1.6m的细绳一端,系一个总质量为m=0.5kg的盛水容器,以绳另一端为圆心,在竖直平面内作圆周运动,如图所示.若“水流星”通过最高点的速度为v=4m/s,则下列哪些说法正确(不计空气阻力,取g=10m/s2)( )
| A.“水流星”通过最高点时,有水从容器中流出 |
| B.“水流星”通过最高点时,绳的张力和容器底受到的压力均为零 |
| C.“水流星”通过最高点时,处于完全失重状态,不受力的作用 |
| D.绳的张力变化范围为0≤T≤30N |

A、B、当绳的张力恰好为零时,对水和容器整体,根据牛顿第二定律:
mg=m
解得:v=
=
=4m/s.
可知,“水流星”通过最高点的速度最小速度为4m/s,绳的张力为零,此时整体的加速度为 a=g,所以水对桶底压力为零,水不会从容器中流出.
故A错误,B正确.
C、“水流星”通过最高点时,仅受重力,处于完全失重状态.故C错误.
D、设容器运动到最低点时的速度大小为v′,根据机械能守恒定律得:
mg?2L+
mv2=
mv′2
解得:v′=
在最低点,根据牛顿第二定律得:T-mg=m
则得:T=6mg=6×0.5×10N=30N,即绳子的张力最大值为30N,所以绳的张力变化范围为0≤T≤30N.故D正确
故选:BD
mg=m
| v2 |
| L |
解得:v=
| gL |
| 10×1.6 |
可知,“水流星”通过最高点的速度最小速度为4m/s,绳的张力为零,此时整体的加速度为 a=g,所以水对桶底压力为零,水不会从容器中流出.
故A错误,B正确.
C、“水流星”通过最高点时,仅受重力,处于完全失重状态.故C错误.
D、设容器运动到最低点时的速度大小为v′,根据机械能守恒定律得:
mg?2L+
| 1 |
| 2 |
| 1 |
| 2 |
解得:v′=
| 5gL |
在最低点,根据牛顿第二定律得:T-mg=m
| v′2 |
| L |
则得:T=6mg=6×0.5×10N=30N,即绳子的张力最大值为30N,所以绳的张力变化范围为0≤T≤30N.故D正确
故选:BD

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目