题目内容
18.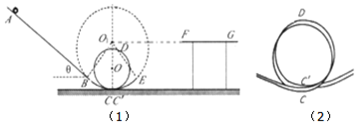 某校科技节期间举办“云霄飞车”比赛,小敏同学制作的部分轨道如图(1)所示,倾角θ=37°的直轨道AB,半径R1=1m的光滑圆弧轨道BC,半径R2=0.4m的光滑螺旋圆轨道CDC′,如图(2)所示,光滑圆轨道CE,水平直轨道FG(与圆弧轨道同心圆O1等高),其中轨道BC、C′E与圆轨道最低点平滑连接且C、C′点不重叠,∠BO1C=∠CO1E=37°.整个轨道在竖直平面内,比赛中,小敏同学让质量m=0.04kg的小球从轨道上A点静止下滑,经过BCDC′E后刚好飞跃到水平轨道F点,并沿水平轨道FG运动.直轨道AB与小球的动摩擦因数μ=0.3,小球可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2,求:
某校科技节期间举办“云霄飞车”比赛,小敏同学制作的部分轨道如图(1)所示,倾角θ=37°的直轨道AB,半径R1=1m的光滑圆弧轨道BC,半径R2=0.4m的光滑螺旋圆轨道CDC′,如图(2)所示,光滑圆轨道CE,水平直轨道FG(与圆弧轨道同心圆O1等高),其中轨道BC、C′E与圆轨道最低点平滑连接且C、C′点不重叠,∠BO1C=∠CO1E=37°.整个轨道在竖直平面内,比赛中,小敏同学让质量m=0.04kg的小球从轨道上A点静止下滑,经过BCDC′E后刚好飞跃到水平轨道F点,并沿水平轨道FG运动.直轨道AB与小球的动摩擦因数μ=0.3,小球可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2,求:(1)小球运动到F点时的速度大小;
(2)小球运动至圆轨道最高点D时对轨道的作用力大小;
(3)A点离水平地面的高度.
分析 (1)小球从E运动到F的过程其逆过程是平抛运动,根据高度求得小球离开E点时竖直分速度,再由分速度关系求出小球运动到F点时的速度大小;
(2)从D到F的过程,运用机械能守恒定律求出小球通过D点的速度.小球运动至圆轨道最高点D时,由重力和轨道的作用力的合力提供向心力,由向心力公式求轨道对小球的作用力,从而得到小球对轨道的作用力大小;
(3)从A到F的过程,由动能定理列式,可求得A点离水平地面的高度.
解答 解:(1)小球从E运动到F的逆过程是平抛运动,设小球离开E点时竖直分速度为vy,小球运动到F点时的速度大小为vF.则有:
vy=$\sqrt{2gh}$=$\sqrt{2g•{R}_{1}cos37°}$=$\sqrt{2×10×1×0.8}$=4m/s
由分速度关系得:tan37°=$\frac{{v}_{y}}{{v}_{F}}$
解得:vF=$\frac{16}{3}$m/s
(2)从D到F的过程,由机械能守恒定律得:
$\frac{1}{2}m{v}_{D}^{2}$+2mgR2=mgR1+$\frac{1}{2}m{v}_{F}^{2}$
在D点,对小球,由向心力公式得:mg+N=m$\frac{{v}_{D}^{2}}{{R}_{2}}$
联立解得:N≈4.64N
由牛顿第三定律知,小球运动至圆轨道最高点D时对轨道的作用力大小为4.64N.
(3)设A点离水平地面的高度为H.从A到F的过程,由动能定理得:
mg(H-R1)-μmgcosθ•$\frac{H-{R}_{1}(1-cos37°)}{sin37°}$=$\frac{1}{2}m{v}_{F}^{2}$-0
解得:H≈3.9m
答:(1)小球运动到F点时的速度大小是$\frac{16}{3}$m/s;
(2)小球运动至圆轨道最高点D时对轨道的作用力大小是4.64N;
(3)A点离水平地面的高度是3.9m.
点评 本题要求同学们能正确分析物体的运动情况,掌握平抛运动的研究方法:运动的分解法.在轨道光滑的情况下,往往运用机械能守恒定律求速度或高度.有摩擦力时往往根据动能定理求高度.


| A. | Ea<Eb,方向相同 | B. | Ea<Eb,方向不同 | C. | Ea>Eb,方向相同 | D. | Ea>Eb,方向不同 |
 一空间有垂直纸面向里的匀强磁场B,两条电阻不计的平行光滑导轨竖直放置在磁场内,如图8所示,磁感应强度B=0.5T,导体棒ab、cd长度均为0.2m,电阻均为0.1Ω,重力均为0.1N,现用力向上拉动导体棒ab,使之匀速上升(导体棒ab、cd与导轨接触良好),此时cd静止不动,则ab上升时,下列说法正确的是( )
一空间有垂直纸面向里的匀强磁场B,两条电阻不计的平行光滑导轨竖直放置在磁场内,如图8所示,磁感应强度B=0.5T,导体棒ab、cd长度均为0.2m,电阻均为0.1Ω,重力均为0.1N,现用力向上拉动导体棒ab,使之匀速上升(导体棒ab、cd与导轨接触良好),此时cd静止不动,则ab上升时,下列说法正确的是( )| A. | ab受到的拉力大小为2 N | |
| B. | ab向上运动的速度为2 m/s | |
| C. | 在2 s内,拉力做功,产生了0.4J的热量 | |
| D. | 在2 s内,拉力做功为0.6 J |
 如图,粗糙水平面上a、b、c、d四个相同小物块用四根完全相同的轻弹簧连接,正好组成一个等腰梯形,系统静止,ab之间、ac之间以及bd之间的弹簧长度相同且等于cd之间弹簧长度的一半,ab之间弹簧弹力大小为cd之间弹簧弹力大小的一半,若a受到的摩擦力大小为f,则下列说法不正确的是( )
如图,粗糙水平面上a、b、c、d四个相同小物块用四根完全相同的轻弹簧连接,正好组成一个等腰梯形,系统静止,ab之间、ac之间以及bd之间的弹簧长度相同且等于cd之间弹簧长度的一半,ab之间弹簧弹力大小为cd之间弹簧弹力大小的一半,若a受到的摩擦力大小为f,则下列说法不正确的是( )| A. | ab之间的弹簧一定是压缩的 | B. | b受到的摩擦力大小为f | ||
| C. | d受到的摩擦力大小为2f | D. | c受到的摩擦力大小为$\sqrt{3}$f |
 如图所示,斜面体A始终静止在水平地面上,质量为m的滑块B在外力F1和F2的共同作用下沿斜面体表面向下运动,F1方向水平向右,F2方向沿斜面体的表面向下,此时斜面体受到地面的摩擦力向左,则下列说法正确的是( )
如图所示,斜面体A始终静止在水平地面上,质量为m的滑块B在外力F1和F2的共同作用下沿斜面体表面向下运动,F1方向水平向右,F2方向沿斜面体的表面向下,此时斜面体受到地面的摩擦力向左,则下列说法正确的是( )| A. | 若只撤去F2,在滑块B仍向下运动的过程中,A所受地面摩擦力变大 | |
| B. | 若只撤去F2,在滑块B仍向下运动的过程中,A所受地面摩擦力不变 | |
| C. | 若只撤去F1,在滑块B仍向下运动的过程中,A所受地面摩擦力的方向可能向右 | |
| D. | 若只撤去F1,在滑块B仍向下运动的过程中,A所受地面摩擦力的方向仍然向左 |
 铁路弯道处内外轨道高度是不同的,已知内外轨道平面与水平面的倾角为θ,转弯处的弯道半径为R,如图所示,若质量为m的火车转弯时速度小于$\sqrt{gRtanθ}$,则( )
铁路弯道处内外轨道高度是不同的,已知内外轨道平面与水平面的倾角为θ,转弯处的弯道半径为R,如图所示,若质量为m的火车转弯时速度小于$\sqrt{gRtanθ}$,则( )| A. | 外轨对外侧车轮有挤压 | |
| B. | 内轨对内侧车轮有挤压 | |
| C. | 这时铁轨对火车垂直于轨道平面的支持力小于$\frac{mg}{cosθ}$ | |
| D. | 这时铁轨对火车垂直于轨道平面的支持力等于$\frac{mg}{cosθ}$ |
 如图所示,质量为4kg的物体静止于水平面上,物体与水平面间的动摩擦因数为0.5,物体在与水平方向成37°的斜向上拉力F的作用下,沿水平面做匀加速运动,已知3S内物体的位移X=2.25m,求(sin37°=0.6,cos37°=0.8,g取10m/s2)
如图所示,质量为4kg的物体静止于水平面上,物体与水平面间的动摩擦因数为0.5,物体在与水平方向成37°的斜向上拉力F的作用下,沿水平面做匀加速运动,已知3S内物体的位移X=2.25m,求(sin37°=0.6,cos37°=0.8,g取10m/s2)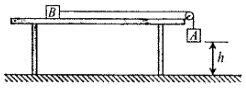 如图所示,物块A、B的质量均为0.2kg,二者用跨过定滑轮的轻细绳连接,将B置于粗糙水平桌面上,使A的下端距离地面的高度为h=0.5m,由静止释放B,A落地瞬间速度大小为v=2m/s,落地后不反弹.已知重力加速度g=10m/s2,滑轮的质量和摩擦均不计,B离滑轮足够远.则A下落的加速度大小为4m/s2;B总共滑行的距离为1.5m.
如图所示,物块A、B的质量均为0.2kg,二者用跨过定滑轮的轻细绳连接,将B置于粗糙水平桌面上,使A的下端距离地面的高度为h=0.5m,由静止释放B,A落地瞬间速度大小为v=2m/s,落地后不反弹.已知重力加速度g=10m/s2,滑轮的质量和摩擦均不计,B离滑轮足够远.则A下落的加速度大小为4m/s2;B总共滑行的距离为1.5m.