题目内容
13.有一辆质量为1t的小汽车驶上圆弧半径为90m的拱桥,(g=10m/s2,R地=6400km)(1)汽车到达桥顶是速度为9m/s,汽车对桥的压力有多大?
(2)汽车以多大速度经过桥顶时恰好对桥没有压力?
(3)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面腾空,速度要多大?
(4)如果发射一颗地球卫星,至少需要多大的速度?
分析 (1)汽车在桥顶,由竖直方向上的合力提供向心力,根据牛顿第二定律求出桥对汽车的支持力,从而得出汽车对桥的压力.
(2)(3)当汽车对桥的压力为零时,竖直方向上仅受重力,根据牛顿第二定律求出汽车的速度;
(4)根据重力提供向心力即可求出.
解答 解:(1)1t=1000kg
根据牛顿第二定律有:mg-N=m$\frac{{v}^{2}}{R}$
则得,N=mg-m$\frac{{v}^{2}}{R}$=1000×10-1000×$\frac{{9}^{2}}{90}$N=9900N.
根据牛顿第三定律得,汽车对桥的压力大小为9900N.
(2)当汽车对桥的压力为零时,有:mg=m$\frac{{v}_{0}^{2}}{R}$
则得,v0=$\sqrt{gR}$=$\sqrt{10×90}$=30m/s
故汽车以20 m/s速度经过桥顶时便恰好对桥没有压力而腾空.
(3)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面腾空时,汽车对桥的压力为零时,有:mg=m$\frac{{v}_{1}^{2}}{{R}_{地}}$
则:${v}_{1}=\sqrt{g{R}_{地}}=\sqrt{10×6400×1{0}^{3}}$=8×103m/s
(4)卫星在地球的表面做圆周运动时需要的发射速度最小,此时:mg=m$\frac{{v}_{2}^{2}}{{R}_{地}}$
所以:v2=v1=8×103m/s
答:(1)汽车到达桥顶时速度为9m/s,汽车对桥的压力是9900N;
(2)汽车以30m/s的速度经过桥顶时恰好对桥没有压力而腾空;
(3)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面腾空,速度要8×103m/s;
(4)如果发射一颗地球卫星,至少需要的速度是8×103m/s.
点评 解决本题的关键知道在桥顶竖直方向上的合力提供汽车运动所需的向心力,会根据牛顿第二定律列出表达式.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 在真空环境内探测微粒在重力作用下运动的简化装置如图所示.P是一个微粒源,能持续水平向右发射质量相同、初速度不同的微粒.高度为h=0.8m的探测屏AB竖直放置,离P点的水平距离为L=2.0m,上端A与P点的高度差也为h,(g取10m/s2).则能被屏探测到的微粒的最大初速度是( )
在真空环境内探测微粒在重力作用下运动的简化装置如图所示.P是一个微粒源,能持续水平向右发射质量相同、初速度不同的微粒.高度为h=0.8m的探测屏AB竖直放置,离P点的水平距离为L=2.0m,上端A与P点的高度差也为h,(g取10m/s2).则能被屏探测到的微粒的最大初速度是( )| A. | 4m/s | B. | 5m/s | C. | 3m/s | D. | 2m/s |
| A. | 物体内分子热运动的平均动能越大,则物体的温度越高 | |
| B. | 液体表面层中分子间的相距作用表现为引力 | |
| C. | 用显微镜观测液体中的布朗运动,观察到的是液体分子的无规则运动 | |
| D. | 电冰箱的制冷系统能够不断把冰箱内的热量传递到外面,违背了热力学第二定律 | |
| E. | 一定质量的理想气体保持体积不变,温度升高,则单位时间内撞击器壁单位面积上的分子数增多 |
 如图所示,在竖直方向上A、B两物体通过轻质弹簧相连,A放在水平地面上,B、C两物体通过细绳绕过光滑轻质定滑轮相连,用手拿住C,使细线刚刚拉直但无拉力作用,并保证滑轮两边的细线竖直.物体A、B、C的质量分别为mA、mB、mC.开始时整个系统处于静止状态,将C从静止释放后,发现C运动到最低点时,A对地面的压力恰好为零,弹簧始终处于弹性限度内,则( )
如图所示,在竖直方向上A、B两物体通过轻质弹簧相连,A放在水平地面上,B、C两物体通过细绳绕过光滑轻质定滑轮相连,用手拿住C,使细线刚刚拉直但无拉力作用,并保证滑轮两边的细线竖直.物体A、B、C的质量分别为mA、mB、mC.开始时整个系统处于静止状态,将C从静止释放后,发现C运动到最低点时,A对地面的压力恰好为零,弹簧始终处于弹性限度内,则( )| A. | C在下降过程中,B、C组成的系统机械能守恒 | |
| B. | B在上升过程中,B的机械能一直增大 | |
| C. | 如果mA>mB,则一定有mC<mB | |
| D. | 当弹簧处于原长时,B、C两物体的动能之和一定最大 |

| A. | a点电势一定小于b点电势 | B. | a点电势一定等于b点电势 | ||
| C. | a点电场强度一定小于b点电场强度 | D. | a点电场强度一定等于b点电场强度 |
 如图所示,某带电粒子由静止开始经电压为U1的电场加速后,射入水平放置、电势差为U2的两块平行导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射人,穿过两板后又垂直于磁场方向射入边界线竖直、磁感应强度为B的匀强磁场中,设粒子射入磁场和射出磁场的M、N两点间的距离为s(不计重力,不考虑边缘效应).下列说法正确的是( )
如图所示,某带电粒子由静止开始经电压为U1的电场加速后,射入水平放置、电势差为U2的两块平行导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射人,穿过两板后又垂直于磁场方向射入边界线竖直、磁感应强度为B的匀强磁场中,设粒子射入磁场和射出磁场的M、N两点间的距离为s(不计重力,不考虑边缘效应).下列说法正确的是( )| A. | 若仅将水平放置的平行板间距增大,则s减小 | |
| B. | 若仅增大磁感应强度B,则s减小 | |
| C. | 若仅增大U1,则s增大 | |
| D. | 若仅增大U2,则s增大 |
 用如图的装置研究光电效应现象,当用光子能量为3.0eV的光照射到光电管上时,电流表G的读数为0.2mA.移动变阻器的触点c,当电压表的示数大于或等于0.7V时,电流表读数为0.则( )
用如图的装置研究光电效应现象,当用光子能量为3.0eV的光照射到光电管上时,电流表G的读数为0.2mA.移动变阻器的触点c,当电压表的示数大于或等于0.7V时,电流表读数为0.则( )| A. | 光电管阴极的逸出功为2.3eV | |
| B. | 所有光电子的初动能为0.7eV | |
| C. | 电键K断开后,仍有电流流过电流表G | |
| D. | 改用能量为1.5eV的光子照射,电流表G也有电流,但电流较小 |
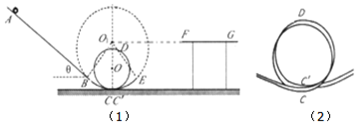 某校科技节期间举办“云霄飞车”比赛,小敏同学制作的部分轨道如图(1)所示,倾角θ=37°的直轨道AB,半径R1=1m的光滑圆弧轨道BC,半径R2=0.4m的光滑螺旋圆轨道CDC′,如图(2)所示,光滑圆轨道CE,水平直轨道FG(与圆弧轨道同心圆O1等高),其中轨道BC、C′E与圆轨道最低点平滑连接且C、C′点不重叠,∠BO1C=∠CO1E=37°.整个轨道在竖直平面内,比赛中,小敏同学让质量m=0.04kg的小球从轨道上A点静止下滑,经过BCDC′E后刚好飞跃到水平轨道F点,并沿水平轨道FG运动.直轨道AB与小球的动摩擦因数μ=0.3,小球可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2,求:
某校科技节期间举办“云霄飞车”比赛,小敏同学制作的部分轨道如图(1)所示,倾角θ=37°的直轨道AB,半径R1=1m的光滑圆弧轨道BC,半径R2=0.4m的光滑螺旋圆轨道CDC′,如图(2)所示,光滑圆轨道CE,水平直轨道FG(与圆弧轨道同心圆O1等高),其中轨道BC、C′E与圆轨道最低点平滑连接且C、C′点不重叠,∠BO1C=∠CO1E=37°.整个轨道在竖直平面内,比赛中,小敏同学让质量m=0.04kg的小球从轨道上A点静止下滑,经过BCDC′E后刚好飞跃到水平轨道F点,并沿水平轨道FG运动.直轨道AB与小球的动摩擦因数μ=0.3,小球可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2,求: