题目内容
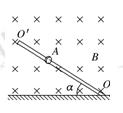
(16分)如图所示,一根长为L的轻绳一端固定在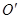 点,另一端系一质量
点,另一端系一质量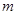 的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。
的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。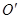 点下方有一以
点下方有一以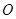 点为顶点的固定斜面,倾角
点为顶点的固定斜面,倾角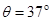 ,斜面足够长,且
,斜面足够长,且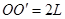 ,已知重力加速度为
,已知重力加速度为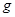 ,忽略空气阻力;求:
,忽略空气阻力;求: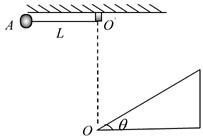
(1)轻绳断时的前后瞬间,小球的加速度? (2)小球落至斜面上的速度大小及方向?
(1)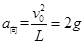 ,方向竖直向上;
,方向竖直向上;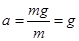 ,方向竖直向下
,方向竖直向下
(2)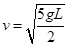 ,与水平面夹角为
,与水平面夹角为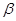 ,
,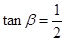
解析试题分析:(1)小球从A到最低点,由动能定理: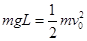 ,得:
,得: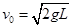 (2分)
(2分)
轻绳断前瞬间,小球的加速度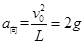 方向竖直向上 (2分)
方向竖直向上 (2分)
轻绳断后瞬间,小球的加速度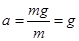 方向竖直向下 (2分)
方向竖直向下 (2分)
(2)以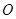 为坐标原点,
为坐标原点,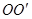 为
为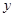 轴,建立直角坐标系,斜面对应方程
轴,建立直角坐标系,斜面对应方程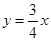 (2分)
(2分)
平抛轨迹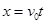
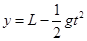 ,消去
,消去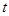 得
得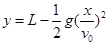 (2分)
(2分)
联立解得: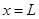
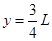 (2分)
(2分)
平抛的高速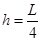 ,
,
小球落至斜面上的速度: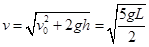 (2分)
(2分)
与水平面夹角为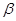 ,
,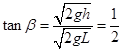 (2分)
(2分)
考点:本题考查了动能定理、牛顿第二定律、平抛运动规律。

练习册系列答案
相关题目
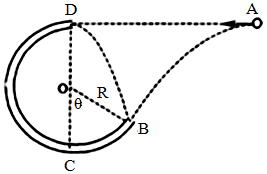
 ,处在水平向右的匀强电场中,一质量为
,处在水平向右的匀强电场中,一质量为 的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低位置B时,球对轨道的压力为
的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低位置B时,球对轨道的压力为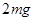 .求:
.求: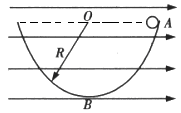
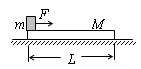

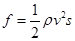 ,式中ρ为大气的密度,v是返回舱的运动速度,s为与形状特征有关的阻力面积。当返回舱距地面高度为10km时打开面积为1200m2的降落伞,直到速度达到8m/s后匀速下落。为实现软着陆(即着陆时返回舱的速度为零),当返回舱离地面1.2m时反冲发动机点火,使返回舱落地的速度减为零,返回舱此时的质量为2.7×103kg。(取g=10m/s2)
,式中ρ为大气的密度,v是返回舱的运动速度,s为与形状特征有关的阻力面积。当返回舱距地面高度为10km时打开面积为1200m2的降落伞,直到速度达到8m/s后匀速下落。为实现软着陆(即着陆时返回舱的速度为零),当返回舱离地面1.2m时反冲发动机点火,使返回舱落地的速度减为零,返回舱此时的质量为2.7×103kg。(取g=10m/s2)
 静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为
静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为 .解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时
.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时 发生弹性碰撞,碰撞后球
发生弹性碰撞,碰撞后球 同一高度,球
同一高度,球 上的
上的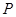 点,
点,  与
与 .已知球
.已知球 ,悬绳长
,悬绳长 ,视两球为质点,重力加速度为
,视两球为质点,重力加速度为 ,不计空气阻力.求:
,不计空气阻力.求: