题目内容
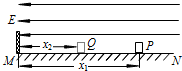
(14分)在方向水平的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点。把小球拉起直至细线与场强平行,然后无初速释放。已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ(如图)。求小球经过最低点时细线对小球的拉力。
mg[3-2cosθ/(1+sinθ)]
解析试题分析:设细线长为l,球的电量为q,场强为E。若电量q为正,则场强方向在题图中向右,反之向左。从释放点到左侧最高点,重力势能的减少等于电势能的增加,
mglcosθ=qEl(1+sinθ) ①
若小球运动到最低点时的速度为v,此时线的拉力为T,由能量关系得
1/2mv2=mgl-qEl ②
由牛顿第二定律得: T-mg=mv2/l ③
由以上各式 : T=mg[3-2cosθ/(1+sinθ)] ④
考点:圆周运动、能量守恒定律、电势能

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
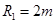 的凹形圆弧轨道和半径
的凹形圆弧轨道和半径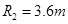 的凸形圆弧轨道三部分组成的模拟滑板组合轨道.这三部分轨道依次平滑连接,且处于同一竖直平面内.其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心O与M点在同一水平面上.可视为质点,质量为
的凸形圆弧轨道三部分组成的模拟滑板组合轨道.这三部分轨道依次平滑连接,且处于同一竖直平面内.其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心O与M点在同一水平面上.可视为质点,质量为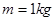 的滑板从斜直轨道上的P点无初速度滑下,经M点滑向N点,P点距水平面的高度
的滑板从斜直轨道上的P点无初速度滑下,经M点滑向N点,P点距水平面的高度 .不计一切阻力,
.不计一切阻力, 取
取 .求:
.求: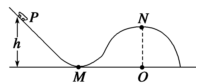
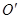 点,另一端系一质量
点,另一端系一质量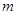 的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。
的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。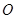 点为顶点的固定斜面,倾角
点为顶点的固定斜面,倾角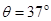 ,斜面足够长,且
,斜面足够长,且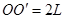 ,已知重力加速度为
,已知重力加速度为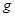 ,忽略空气阻力;求:
,忽略空气阻力;求: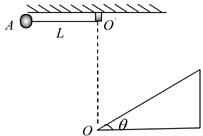



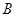 =0.80m的轻绳一端固定在
=0.80m的轻绳一端固定在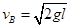 点,另一端连接一质量
点,另一端连接一质量 距离水平地面的高度H = 1.00m。开始时小球处于
距离水平地面的高度H = 1.00m。开始时小球处于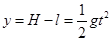 点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到
点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到 正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求:
正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求: 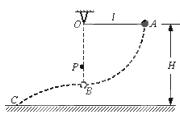
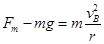 点时的速度大小;
点时的速度大小;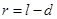 点抛出并落在水平地面的C点,求C点与
点抛出并落在水平地面的C点,求C点与 点之间的水平距离;
点之间的水平距离;