题目内容
【题目】如图所示,一竖直放置的轻弹簧两端各拴接一个物块A和B,整个系统处于静止状态。已知物块A的质量为 mA=2kg,物块B的质量为 mB=4kg,轻弹簧的劲度系数k=100N/m。现对物块A施加一竖直向上的力F,使A从静止开始向上做匀加速直线运动,经t=1.0s物块B刚要离开地面。设整个过程中弹簧始终处于弹性限度内,重力加速度g取10m/s2。求:
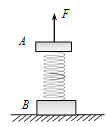
(1)物块B刚要离开地面时,物块A上升的距离x;
(2)此过程中所加外力F的最小值F1和最大值F2的大小。
【答案】(1)0.6m(2)2.4N 62.4N
【解析】(1)A原来静止时,对A有 mAg=kx1 ①
当B刚要离开地面时,对B有 mBg=kx2 ②
此过程中物块A上升的距离 x= x1+x2=0.6m
(2)当物块A开始做匀加速运动时,拉力F最小。
对物块A有 F1+kx1-mAg=mAa ③
即 F1 =mAa
当物块B刚要离开地面时,拉力F最大。
对物块A有 F2-kx2-mAg=mAa ④
即 F2-(mA+ mB)g=mAa
物块A做匀加速直线运动,有![]() ⑤
⑤
联立③④⑤式解得:F1=2.4N,F2=62.4N

练习册系列答案
相关题目