Question

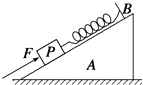
【题目】如图所示，质量为M的小车静止在光滑的水平地面上，车上装有半径为R的半圆形光滑轨道．现将质量为m的小球放于半圆形轨道的边缘上，并由静止开始释放，当小球滑至半圆形轨道的最低点位置时，小车移动的距离为 ， 小球的速度为 ．

Answer 1

【答案】；
【解析】解：当小球滚到最低点时，设此过程中

小球水平位移的大小为s1，车水平位移的大小为s2．

在这一过程中，由系统水平方向总动量守恒得（取水平向左为正方向）

m ﹣M =0

又 s1+s2=R

由此可得：s2=

当小球滚至凹槽的最低时，小球和凹槽的速度大小分别为v1和v2．据水平方向动量守恒

mv1=Mv2

另据机械能守恒得：mgR= mv12+ Mv22

得：v1=

所以答案是： ； ．

【考点精析】认真审题，首先需要了解动量守恒定律(动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变)．