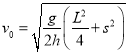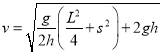��Ŀ����
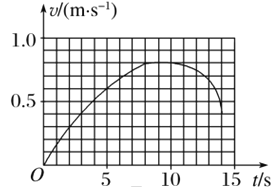
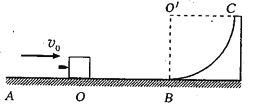
����Ŀ����ͼ��ʾ�����£��ǹ⻬��Բ�ι������ֱ�����ϣô�����ֱ����Ϊ0.8�����뾶�ϣ´���ˮƽ��������Ϊ����С���ԣ����Գ��ٶȣ�ˮƽ���룬��
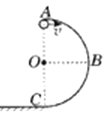
��1����ʹС���ع���˶�����ˮƽ���ٶȣ�����Сֵ�Ƕ��٣�
��2����С���ˮƽ���ٶȣ�С�ڣ�1���е���Сֵ��С�������ܾ����µ㣿���ܣ����ˮƽ���ٶȴ�С����������������ܣ���˵�����ɣ�����ȡ10������2��С��������ʱ��������ʧ����������
���𰸡���1��2������2��2���������![]() ������
������
����������1����С��պ����ڹ������Բ���˶�ʱ��ˮƽ���ٶȣ���С����ʱ��![]() ��
��
�ʣ���![]() ��
��![]() ��2������
��2������
��2�������ٶȣ���������С����ƽ���˶�����������ֱλ��Ϊ�ҵ�ʱ���ڣ���ˮƽλ�ƣ����ң�С��ɽ����������µ㣮������ֱλ��Ϊ��ʱ��ˮƽλ��ҲǡΪR����ң�![]() ���2��
���2��
�ң���������
��������![]() ��
��![]() ������
������
��ˣ����ٶ�����2���������![]() ������ʱ��С�����ƽ���˶������µ㣮
������ʱ��С�����ƽ���˶������µ㣮

��ϰ��ϵ�д�
�����Ŀ