题目内容
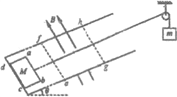
【题目】甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动．质点甲做初速度为零，加速度大小为a1的匀加速直线运动；质点乙做初速度为v0，加速度大小a2为的匀减速直线运动到速度减为零并保持静止．选甲、乙的出发位置为位移零点，甲、乙两质点在运动过程中的位置—速度（x—v）图象如图所示，虚线与对应的坐标轴垂直．
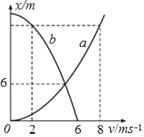
（ⅰ）在x—v图象中，甲质点的运动是哪一图线表示？质点乙的初速度v0是多大？
（ⅱ）求质点甲、乙的加速度大小a1、a2．
【答案】（1）甲
（2）
【解析】试题分析：（1）设运动过程中甲、乙的速度分别为v1、v2，根据速度与位移关系有：v12=2a1x1
得：
可知其图象应为抛物线，且开口向上，故图线a表示质点甲的运动
（2）由v02-v22＝2a2x2
得：
可知其图象应为抛物线，且开口向下，故图线b表示质点乙的运动，且当v2=v0=6m/s时，x=0，从图象可知：v0=6m/s
（3）由图象交点可知，v1=v2时两质点的位移相同，且x=6m，有：
对质点甲：v2=2a1x，
对质点乙：v2-v02=-2a2x
解得： a1+a2=3m/s2
另据图象可知当v1=8m/s，v2=2m/s时，两质点的位移x′相同，有：
对质点甲：v12=2a1x′
对质点乙：v02v22=-2a2x′
解得 a1=2a2
联立可得：a1=2m/s2，a2=1m/s2
练习册系列答案
相关题目
